Hejného metoda výuky matematiky

V roce 1974, po rozporu s učitelkou svého syna ohledně způsobu výuky, začal Milan Hejný společně s několika spolupracovníky v Bratislavě zpracovávat poznatky svého otce. Vít Hejný, otec Milana Hejného, analyzoval příčinu, proč se jeho žáci nesnaží porozumět problémům a místo toho si raději pamatují vzorečky, které jsou ale vhodné pouze pro řešení standardních úloh. Hledal proto úlohy nestandardní a ty experimentálně testoval na žácích a na svém synovi. Myšlenky profesora Hejného a jeho pracovní skupiny byly publikovány v roce 1987 v Bratislavě.[1] Metoda byla zaměřena na budování sítě mentálních matematických schémat při výuce matematiky, které si každý žák tvoří řešením vhodných úloh a diskusí o svých výsledcích se spolužáky, nikoli řešením standardních úloh.

V devadesátých letech profesor Hejný pracoval na Pedagogické fakultě UK a postupně vytvořil tým, se kterým začal přibližovat metodu jiným pedagogům prostřednictvím seminářů na toto téma. V roce 2007 pracovní skupina vedená profesorem Hejným začala pracovat nad řadou učebnic pro první stupeň základních škol, které byly schváleny MŠMT a jsou teď vydávány Nakladatelstvím Fraus. V roce 2013 Milan Hejný založil společnost H-mat, cílem které je metodu rozvíjet a šířit.[1]

Hejného metoda je založena na respektování 12 základních principů[2], které jsou poskládány do uceleného konceptu tak, aby děti objevovaly matematiku samy a s radostí.

Budování schémat

Budování schémat matematických pojmů, jevů, procesů a situací v mysli každého žáka je podstatou vyučovací metody. V Hejného metodě se využívají například schémata autobusu, krokování, rodiny apod., která si děti v dětství samy vytvořily. Děti jsou samy schopny pomocí těchto schémat objevovat svět, dojít k autonomnímu poznání a spojit si je s matematickými problémy. Následně si dítě všimne, že se principy opakují, abstrakci provede samo a intuitivně, čímž se mu vytvoří schéma daného problému nebo pojmu, které je jemu vlastní a přirozené.

Práce v prostředích

Prostředí, jež se skládá z dětem známých nebo představitelných vybraných situací, obsahuje série na sebe navazujících úloh se stejným námětem. V úlohách, které vybízejí k experimentování a k objevování, se vyskytují různé matematické jevy. S náměty jednotlivých prostředí se žáci seznamují v jednoduchých úlohách (simulované obrázky v učebnici a pracovním sešitě, vystřihovánky apod.), postupně pak úlohy gradují, pomocí čehož se prostředí obohacuje a rozšiřuje. Děti v prostředích pracují opakovaně, tím se jim prostředí stává známým, nabývají zde jistoty, ztrácejí strach z matematiky, vzájemně diskutují a korigují myšlenky.

Prolínání témat

Informace spolu logicky souvisejí. V různých prostředích či úlohách děti poznávají jednotlivé pojmy, procesy, řešitelské strategie, jevy, vazby a k jejich dobrému porozumění dojde poskládáním střípků mozaiky dílčích poznatků z jednotlivých prostředí a z různých činností.

Rozvoj osobnosti

Hejného metoda podporuje samostatné uvažování dětí. Jednou z hlavních motivací profesora Hejného při vytváření nové metody byl důraz na to, aby se děti nenechaly v životě manipulovat. Proto učitel ve výuce nepředává hotové poznatky, ale učí děti především argumentovat, diskutovat a vyhodnocovat. Děti pak samy o sobě vědí, co je pro ně správné, respektují druhého a umějí rozhodovat. Dokonce statečně nesou i důsledky svého konání. Vedle matematiky přirozeně objevují také základy sociálního chování a mravně rostou.

Skutečná motivace

Všechny matematické úlohy jsou v Hejného metodě postaveny tak, aby jejich řešení děti „automaticky“ bavilo. Správná motivace je ta, která je vnitřní, ne nucená zvenčí. Děti přicházejí na řešení úkolů díky své vlastní snaze. Motivace dává poznávacímu procesu energii i orientaci, a proto hraje klíčovou roli v kvalitě celého procesu učení. Dítě s vnitřní potřebou poznávat poznává intenzivněji, hlouběji a komplexněji než to, které je k poznávání donuceno.

Reálné zkušenosti

Hejného metoda je založena na vlastních zážitcích dítěte. Výuka matematiky, která je orientována na budování schémat, vychází především z vlastní zkušenosti dětí. Při řešení úloh sbírají děti různé matematické zkušenosti. Pro změnu výhodou sbírání zkušeností je skutečnost, že žák ji získá i tehdy, když úlohu nevyřeší a zapamatuje si postup, jakým se k výsledku nedostane. Samotný fakt, že úlohu řeší, že jakkoli mentálně pracuje, je žákovi přínosný.

Radost z matematiky

Radost z vlastních úspěchů pomáhá i v další výuce. Děti získávají pravou motivaci z pocitu úspěchu, jak dobře vyřešily přiměřeně náročný úkol. Obtížnost úloh je nastavena tak, aby i slabší žáci mohli prožít radost z úspěchu. Dostávají úlohy s obtížností přiměřenou jejich dovednostem.

Vlastní poznatek

Podle profesora Hejného má vlastní poznatek větší váhu než převzatý od někoho jiného. Matematiku podle této metody žák objevuje. Cesta k objevu jde od zkušenosti k pojmu. Žák sbírá celou řadu zkušeností, o kterých dále mluví a konzultuje je se svými spolužáky. Pokud je žák v nějaké matematické oblasti slabší, mohou mu pomoci jeho spolužáci v diskusi zavedené učitelem.

Role učitele

Učitel je moderátor a průvodce diskusí. Je ten, kdo organizuje hodinu, pobízí žáky k práci, zadává vhodné úlohy, raduje se s žáky z jejich objevů a řídí jejich diskuse. Plánuje a realizuje vyučovací hodiny, ve kterých hlídá, aby měl každý práci. Citlivě reaguje na aktuální situaci mezi žáky — individualizuje: snižuje či zvyšuje úroveň obtížnosti dané úlohy podle toho, jak se kterému žákovi právě daří, umožňuje práci jednotlivě či ve skupinách podle volby žáků.

Práce s chybou

Chyba nesmí žáka odradit. Chyba může a měla by být pro žáka užitečnou zkušeností. Úlohou učitele je pomoci žákovi se z chyb poučit. Učitel, který žáka za chybu kárá, mu poznávání nových věcí neusnadňuje. Dítě jí ale samo musí objevit a také musí pochopit, proč se jí dopustilo, chyba se tak stává prostředkem k učení.

Přiměřené výzvy

Učebnice, které byly sestaveny podle Hejného metody, obsahují úlohy pro žáky všech úrovní. Úlohy jsou odstupňovány podle obtížnosti, což má pozitivní vliv na sebehodnocení děti. Tím, že slabší žáci vždy nějaké úlohy vyřeší, předcházíme pocitům úzkosti a hrůzy z dalších hodin matematiky.

Podpora spolupráce

Poznatky se rodí díky diskusi. Děti pracují ve skupinkách, po dvojicích nebo i samostatně. Každý žák je tak schopen říci, jak k výsledku došel, a umí to vysvětlit i druhým. Ostatní si z jeho postupu mohou vzít příklad a tím si rozšiřují své poznatky. Výsledek se rodí na základě spolupráce.

Výsledky výzkumu srovnávacích testů společnosti Kalibro

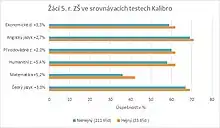
Matematika je vyučována tzv. Hejného metodou na 1. stupni již na přibližně pětině základních škol. Tento způsob výuky ale v poslední době čelí zvýšené kritice, která tvrdí, že tato metoda vede k obecně nižší kvalitě výuky matematiky nebo že je vhodná pouze pro vybrané skupiny žáků. Výsledky žáků ve 244 základních školách, kteří v roce 2018 absolvovali anonymní srovnávací testy společnosti Kalibro Projekt, s. r. o., v pátých třídách, však ukazují zcela něco jiného: Žáci vzdělávaní tzv. Hejného metodou dosahují v testech naopak spíše lepších výsledků než jejich vrstevníci, resp. v žádném případě v matematice (a ani v jiných předmětech) nezaostávají. Tyto údaje ale kritiky nepřesvědčily. Podle jejich názoru je Hejného metoda aplikována na školách se vzdělanějšími rodinami, a proto je nelze srovnávat s obecnějšími školami.[3] Diskutabilní zůstává i otázka nestrannosti a objektivity provedeného srovnávacího testu, neboť společnost Kalibro Projekt, s. r. o., je z 50 % vlastněna vydavatelstvím Fraus, které je jediným vydavatelem učebnic Hejného metody. Vydavatelství Fraus tvrdí, že šetření proběhlo zcela nezávisle.[4]

Testy České školní inspekce žáků pátých tříd také ukázaly, že žáci vyučovaní podle Hejného metody dosahují mírně lepších výsledků než ostatní, ale představitelé Jednoty českých matematiků a fyziků tvrdí, že děti s alternativním přístupem nezvládají ve srovnání s ostatními základní počty a jsou příliš pomalé.[5] Česká školní inspekce ale oponuje, že “za daleko významnější považují utváření pozitivního vztahu k matematice“.[6]

Výsledky Hejného metody a její samotné použití na českých školách jsou předmětem dlouhodobějšího sporu a mají hodně kritiků.[7][8] Metodu kritizovali kromě jiného někteří matematici, podle nichž je její zavádění do škol bez dostatečných dat o dosahovaných výsledcích nebezpečným experimentem;[9] podle Vlastimila Dlaba může dokonce vyvolat duševní poruchy u žáků[10] a v podstatě se ani nejedná o novou metodu – spíše o sebrání zkušeností dobrých učitelů.[11] Předseda Společnosti učitelů matematiky Eduard Fuchs v minulosti uvedl, že metoda bude vždy menšinová a při nepochopení podstaty jsou výsledky neradostné.[12] Podle některých hlasů děti zaostávají například v počtech a násobilce.[13][14] Metoda byla v minulosti předmětem různých argumentačních duelů[14][15] a prověřování jejích výsledků.[16]

O metodě vyšlo hodně publikací, článků ve vědeckých časopisech a konferenčních příspěvků[1], například:

Hejný: Vyučování matematice na 1. stupni ZŠ orientované na budování schémat: Aritmetika.

Hejný a kol.: Teória vyučovania matematiky 2.

Hejný, Kuřina: Dítě, škola a matematika: konstruktivistické přístupy k vyučování.

Hejný, Novotná, Stehlíková: 25 kapitol z didaktiky matematiky.

Bachratý: Archiv Víta Hejného.

Hejný, Jirotková: Contribution of geometry to the goals of education in mathematics.

Hejný: Exploring the Cognitive Dimension of Teaching Mathematics through Scheme-oriented Approach to Education.

Kvasz: Princípy genetického konštruktivizmu.