Gama funkce
Gama funkce (někdy také označovaná jako Eulerův integrál druhého druhu) je zobecněním faktoriálu pro obor komplexních čísel. Používá se v mnoha oblastech matematiky, především pro popis některých rozdělení ve statistice.
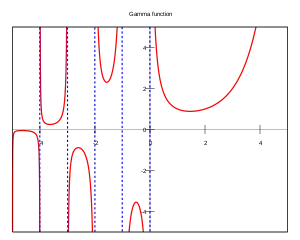
Funkce je značena pomocí řeckého písmene gama a je definována jako holomorfní rozšíření integrálu:
Ačkoliv integrál samotný konverguje jen je-li reálná část z kladná, gama funkce je definována pro libovolné komplexní (a tedy i reálné) číslo, kromě nuly a celých záporných čísel (−1, −2, …).
Vlastnosti
Funkce je spojitá pro . Funkce diverguje pro celá . Tyto body jsou póly prvního řádu a odpovídající rezidua jsou . Jiné singularity nemá a jedná se tedy o funkci meromorfní v celém oboru .
Pro n-tou derivaci platí vztah
- .
V oblasti kladných reálných čísel má gama funkce minimum v bodě .
Užitečné vztahy
- Pro přirozená čísla platí
Některé hodnoty
(nedefinováno) (nedefinováno) (nedefinováno)
Grafy
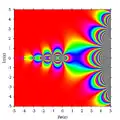 Reálná část Γ(z)
Reálná část Γ(z)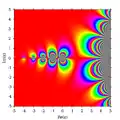 Imaginární část Γ(z)
Imaginární část Γ(z)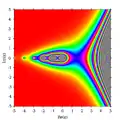 Absolutní hodnota Γ(z)
Absolutní hodnota Γ(z) Absolutní hodnota Γ(z), 3D pohled
Absolutní hodnota Γ(z), 3D pohled
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu gama funkce na Wikimedia Commons
Obrázky, zvuky či videa k tématu gama funkce na Wikimedia Commons - Gama funkce v encyklopedii MathWorld (anglicky)
- Online kalkulátor Gama funkce