Eulerova cihla
Eulerova cihla, pojmenovaná po Leonhardu Eulerovi, je v matematice kvádr, jehož hrany i stěnové úhlopříčky mají celočíselnou délku.
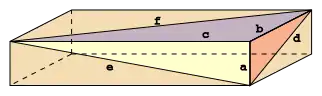
Eulerova cihla
Příklady
Nejmenší Eulerova cihla, nalezena Paulem Halckem v roce 1719, má délky hran 240, 117 a 44.
Další možné délky stran jsou:
- 275, 252 a 240,
- 693, 480 a 140,
- 720, 132 a 85,
- 792, 231 a 160
Perfektní kvádr
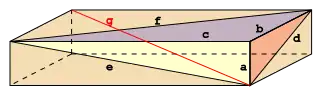
Perfektní kvádr je Eulerova cihla
Perfektní kvádr je Eulerova cihla, jejíž tělesová úhlopříčka má taktéž celočíselnou délku.
Jinak řečeno, je to řešení pro následující soustavu diofantických rovnic:
Zatím nebyl žádný nalezen, ale nebylo ani dokázáno, že žádný takový neexistuje, avšak pokud ano, jedna z jeho stran musí být větší než 1012.
Reference
V tomto článku byl použit překlad textu z článku Euler brick na anglické Wikipedii.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.