Catalanova čísla

Základní rekurentní rovnicí pro výpočet n-tého Catalanova čísla je

${\displaystyle C_{0}=1}$

${\displaystyle C_{n+1}=\sum _{i=0}^{n}C_{i}\,C_{n-i}\quad {\mbox{pro }}n>0}$

Tato rekurence přímo vyvstává z většiny dále uváděných kombinatorických úloh. Například v případě počítání počtu binárních stromů vyjadřuje skutečnost, že binární strom na n vrcholech můžeme postavit buď tak, že do levého podstromu umístíme n vrcholů a do pravého žádný, nebo že do levého podstromu umístíme n-1 vrcholů a do pravého jeden, atd. Výše uvedená suma sčítá počet možností přes všechny takovéto alternativy.

Pro praktické počítání je možná výhodnější tento otevřený tvar:

${\displaystyle C_{0}=1}$

${\displaystyle C_{n+1}={\frac {2(2n+1)}{n+2}}C_{n}\quad {\mbox{pro }}n>0}$

V úvodu uvedený uzavřený předpis ${\displaystyle C_{n}={\frac {1}{n+1}}{2n \choose n}}$ není zcela triviální odvodit (viz dále). Jako alternativu je vhodné uvést vzorec

${\displaystyle C_{n}={2n \choose n}-{2n \choose n-1}}$

Je z něj dobře vidět, že všechna Catalanova čísla jsou celá, což z prvně uvedeného není zřejmé. Odvození tohoto druhého vzorce z prvního je jednoduché:

${\displaystyle {\frac {1}{n+1}}{2n \choose n}={\frac {(2n)!}{(n+1)n!n!}}={\frac {(n+1)(2n)!-n(2n)!}{(n+1)n!n!}}={\frac {(2n)!}{n!n!}}-{\frac {(2n)!}{(n-1)!(n+1)!}}={2n \choose n}-{2n \choose n-1}}$

• Počet zakořeněných binárních stromů s n listy je ${\displaystyle C_{n-1}}$.

Příklad catalanových číset v binárním strome

• Počet korektních uzávorkování 2n závorek je ${\displaystyle C_{n}}$.

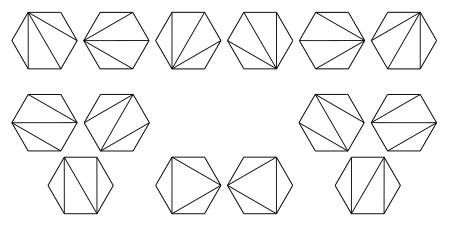
• Počet triangulací konvexního n-úhelníka je ${\displaystyle C_{n-2}}$. Toto je ukázka pro n=6 (${\displaystyle C_{4}=14}$).

Příklad CAtalanových čísel v n-úhelníku

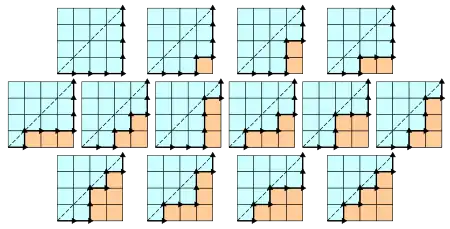
• Počet způsobů, jak se v mřížce n×n dostat z levého dolního do pravého horního rohu, aniž bychom překročili diagonálu nebo se vraceli, je ${\displaystyle C_{n}}$.

Catalovy čísla v mřížce 4×4