Bernoulliho–Navierova hypotéza
Bernoulliho–Navierova hypotéza (také Navierova–Bernoulliho hypotéza či Eulerova–Bernoulliho hypotéza) je v mechanice pružnosti a pevnosti předpoklad pro ohýbaný prvek. Tato hypotéza předpokládá, že průřez, který je před deformací rovinný, zůstává rovinný i po deformaci, resp. průřezy po deformaci zůstávají kolmé na deformovanou střednici prutu. Hypotéza je pojmenována po Jacobu Bernoullim, Danielu Bernoullim a Claude-Louisi Navierovi, případně po Leonhardu Eulerovi.
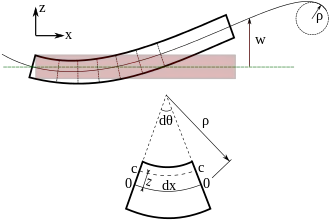
Platnost
Hypotéza obecně platí pro dostatečně štíhlé pruty, naopak pro prvky, u nichž je výška průřezu řádově podobně velká jako délka, je nutno použít pokročilejší teorie deformace (Mindlin, Timošenko). Platnost je dále omezena na izotropní (či ortotropní) materiály, které jsou lineárně pružné; zároveň musejí být pruty v daném průřezu homogenní (a po délce příliš neměnit svůj průřez). Vzniklá přetvoření na prutu taktéž musejí být malá.
Pokud jsou předešlé podmínky splněny, pro průhyb platí:
Druhá derivace průběhu průhybu prutu podle délky , vyjádřená jako křivost prutu, je rovna zlomku, kde je Youngův modul pružnosti, je moment setrvačnosti průřezu a je vnitřní ohybový moment.
Pro nosník, který je vyroben z homogenního materiálu po celé své délce a má navíc konstantní průřez, lze za použití Schwedlerovy věty z předchozí rovnice získat závislost průhybu na spojitém zatížení :
Normálové napětí
Základní vzorec pro výpočet normálového napětí od působícího ohybového momentu, který platí díky BN hypotéze, je následující:[1]
Použité veličiny:
- normálové napětí v průřezu
- – ohybový moment kolem neutrální osy
- – kolmá vzdálenost vláken k neutrální ose
- – moment setrvačnosti k neutrální ose y
- – průřezový modul k neutrální ose y.
Deskové konstrukce
U deskových konstrukcí je rozšíření Bernoulliho–Navierovy hypotézy nazýváno jako Kirchhoff–Loveho teorie.
Odkazy
Reference
- Gere, J. M. Timoshenko, S.P. Mechanics of Materials. PWS Publishing Company: 1997.