Zhlukovanie
Zhlukovanie[1] (clustering, mapovanie, sieťovanie, triedenie) je metóda hľadania súvislostí v celku a následné utriedenie objektov na základe podobných vlastností do zhlukov. Je základom napríklad pri dolovaní dát alebo pri štatistickej dátovej analýze. Používa sa najmä v strojovom učení.
Zhlukovanie samotné je skôr spôsob riešenia ako konkrétny algoritmus. Rôzne algoritmy sa líšia v spôsobe riešenia ako určiť, čo zhluk je a ako ho nájsť. Najčastejšie sa zhluk definuje ako skupina s malými vzdialenosťami medzi objektmi, zhustené dáta v dátovom priestore alebo štatistické distribúcie. Použitie príslušného algoritmu zhlukovania (vrátane funkcie vzdialenosti, prah hustoty alebo počet očakávaných zhlukov) závisí od individuálnych údajov a očakávaných výsledkov. Zhlukovanie ako také nie je samostatná úloha ale opakujúci sa proces získavania vedomostí a interaktívna objektová optimalizácia. Často je potrebné predspracovanie dát a upravenie dát modelu aby boli dosiahnuté požadované výsledky.
Zhluky a zhlukovanie
Podľa Vladimíra Estivilla Castrova sa pojem „zhluk“ nedá presne definovať, čo je jeden z dôvodov prečo existuje toľko algoritmov zhlukovania.[2] K dispozícii je spoločný menovateľ: skupina dátových objektov. Rôzni výskumníci používajú rôzne modely zhlukov a to vedie k používaniu rôznych typov algoritmov. Pojem zhluk v rôznych algoritmoch sa výrazne líši vo svojich vlastnostiach. Pochopenie týchto modelov zhlukov vedie k pochopeniu rôznych algoritmov zhlukovania. Typické modely zhlukov:
- Modely na základe spojenia – napríklad hierarchické zhlukovanie určuje modely na základe vzdialenosti prepojení jednotlivých dát v dátovom priestore.
- Ťažiskové modely – napríklad k-means algoritmus predstavuje každý zhluk ako jednotlivý priemerný vektor.
- Distribučné modely – Klastre sú modelované použitím štatistických distribúcií, ako viacrozmerné normálne rozdelenie používaného algoritmom očakávaného maxima.
- Modely hustoty – napríklad DBSCAN a optika definuje zhluky ako regióny zhustených dát v dátovom priestore.
- Pod priestorové modely – v Biclustering (tiež známy ako multi-zhlukovanie alebo duálne zhlukovanie), zhluky sú modelované oboma členmi zhluku a ich parametrami.
- Skupinové modely – niektoré algoritmy neposkytujú prepracovaný model pre výsledky, poskytujú len informácie o zoskupení dát.
"Zhlukovanie" je v podstate súbor týchto skupín, obvykle obsahujúci všetky objekty v dátovom priestore. Okrem toho môže stanoviť vzťah zhlukov navzájom, napríklad hierarchiu zoskupenia zhlukov vložených do seba. Zhluky možno zhruba rozlíšiť:
- Ťažké zhlukovanie – objekt buď do zhluku patrí alebo nie
- Mäkké zhlukovanie (tiež: Fuzzy zhlukovanie) – každý objekt patrí ku každému zhluku do istej miery (napr. pravdepodobnosť, že sa objekt v zhluku nachádza)
Jemné rozdelenie zhlukovania:
- Striktné rozdelenie zhlukovania – každý objekt patrí do práve jedného zhluku
- Striktné rozdelenie zhlukovania v extrémnych prípadoch – objekty sa môžu vyskytovať aj samostatne – nepatria do žiadneho zhluku.
- Prekrývajúce sa zhlukovanie (tiež: alternatívne zhlukovanie) – objekty môžu patriť do viac ako jedného zhluku.
- Hierarchické zhlukovanie – ak objekt patrí do zhluku tak aj potomok tam bude patriť.
- Podpriestor zhlukovania – pri prekrývaní zhlukov v rámci jednoznačne definovaného podpriestoru, sú klastre neočakávane prekrývané.
Algoritmy zhlukovania
Algoritmy môžu byť triedené na základe modelu zhluku. Uvedené sú len najvýznamnejšie príklady algoritmov zhlukovania. Neexistuje objektívny (správny) algoritmus zhlukovania, ale ako bolo poznamenané „zhluk je v oku pozorovateľa.“[2] Najvhodnejší model pre zhlukovanie je často treba zvoliť experimentálne ak nie je matematický dôvod preferovať jeden model zhluku pred iným. Je potrebné poznamenať, že algoritmus, ktorý je určený pre jeden typ modelov nemá šancu na dátový súbor, ktorý obsahuje radikálne odlišný model.[2] Napríklad, k-means nenájde non-konvexné zoskupenie.[2]
Zhlukovanie na základe spojenia (hierarchické zhlukovanie)
Zhlukovanie na základe spojenia, tiež známe ako hierarchické zhlukovanie je založené na základnej myšlienke, že objekty sú viac príbuzné blízkym predmetom ako objektom vo väčšej vzdialenosti. Tieto algoritmy spájajú objekty do zhlukov na základe ich vzdialeností. Zhluk môže byť opísaný predovšetkým maximálnou vzdialenosťou potrebnou pre prepojenie všetkých častí zhluku. Pri rôznych vzdialenostiach sa vytvoria rôzne zhluky, čo vysvetľuje odkiaľ pochádza spoločný názov „hierarchické zhlukovanie“: tieto algoritmy neposkytujú len obyčajné rozdelenie dátového súboru, ale rozsiahlu hierarchiu zhlukov, ktoré sú na seba napojené v rôznych vzdialenostiach. V dendograme, os y označuje vzdialenosť v ktorej sa zhluky zlučujú a objekty sú poukladané na ose x aby sa zhluky nemiešali.
Zhlukovanie na základe spojenia je celý rad metód, ktoré sa líšia podľa toho, ako sú počítané vzdialenosti. Okrem obvyklej voľby, akú funkciu vzdialenosti použiť, musí užívateľ rozhodnúť aké kritérium väzieb (čím viac objektov obsahuje zhluk, tým viac kandidátov na vypočítanie vzdialenosti) použiť. Najpopulárnejšie možnosti: jednoväzbové zhlukovanie (minimálne vzdialenosti objektu), kompletné združovanie väzieb (maximálne vzdialenosti objektu) alebo UPGMA („Unweighted Pair Group Method with Arithmetic Mean“, tiež známe ako priemerné väzbové zhlukovanie). Okrem toho môže byť hierarchické zhlukovanie aglomeratívne (počínajúc jednotlivými prvkami a ich agregáciou do zhlukov), alebo deliace (počínajúc kompletnou sadou dát, ktorú delia na oddiely).
Tieto metódy nebudú vyrábať jedinečné rozdelenie dátového súboru, ale hierarchiu, z ktorej užívateľ musí zvoliť vhodné zhluky. Nie sú príliš robustné na odľahlých, čo sa buď zobrazí ako ďalšie zhluky alebo môže dokonca spôsobiť ďalšie zlučovanie zhlukov (známy ako fenomén „reťazenia“, najmä pri jednoväzbových algoritmoch). Vo všeobecnom prípade, je zložitosť O (n3), čo je príliš pomalé pre veľké súbory dát. Pre špeciálne prípady sú známe niektoré efektívne metódy (zložitosť O (n2)): SLINK[3] pre jednoväzbové a CLINK[4] pre viacväzbové zhlukovanie. V spoločnosti dolovania dát sú tieto metódy známe ako teoretický základ zhlukovej analýzy, ale často považované za zastarané. Poskytujú však inšpiráciu pre mnoho ďalších metód ako napríklad zhlukovanie na základe hustoty.
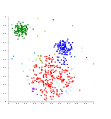 Jednoväzbové zhlukovanie na Gaussových dátach.
Jednoväzbové zhlukovanie na Gaussových dátach.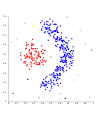 Jednoväzbové zhlukovanie na modeloch na základe hustoty.
Jednoväzbové zhlukovanie na modeloch na základe hustoty.
Zhlukovanie na základe ťažiska (K-means zhlukovanie)
Pri zhlukovaní na základe ťažiska sú zhluky reprezentované ústredným vektorom, ktorý nemusí byť nutne členom súboru dát. Ak je počet zhlukov vopred daný (k), k-means zhlukovanie poskytuje formálnu definíciu ako optimalizačný problém: nájsť centrá zhlukov a priradiť objekty k najbližším centrám, tak, že druhé mocniny vzdialeností od centier zhlukov sú minimálne.
Optimalizačný problém je sám o sebe známy, že je NP-hard, a tak sa hľadá iba približné riešenie problému. Dobre známou metódou približného riešenia je Lloydov algoritmus *, často nazývaný aj „k-means algoritmus“. To však nájde len miestne optimum a obyčajne sa spúšťa viackrát s rôznymi náhodnými inicializáciami. Variácie k-means často zahŕňajú tak optimalizáciu ako aj výber najlepšej možnosti viacnásobného spustenia, ale tiež obmedzuje ťažiská členom súboru dát (k-medoids), výber mediánov (k-medians), výber počiatočných ťažísk menej náhodne (k-means ++) alebo umožňujú fuzzy priradenie zhlukov (Fuzzy k-means).
Väčšina algoritmov typu k-means vyžaduje určenie počtu zhlukov (k) vopred, čo je považované za najväčšiu nevýhodu týchto algoritmov. Navyše preferujú zhluky približne rovnakej veľkosti, pretože priradzujú objekt najbližšiemu ťažisku. To často vedie k nesprávnemu určovaniu hraníc medzi zhlukmi (čo nie je prekvapujúce, keďže k-means optimalizuje centrá zhlukov, nie hranice).
K-means má rad zaujímavých teoretických vlastností. Na jednej strane rozdeľuje dátový priestor do štruktúry známej ako Voronoiového diagram. Na druhej strane je koncepčne blízky klasifikácii najbližšieho suseda, a ako taký je populárny v strojovom učení. Po tretie, môže byť považovaný za variáciu klasifikácie na báze modelov, a Lloydov algoritmus ako variáciu algoritmu očakávaného maxima pre model uvedený nižšie.
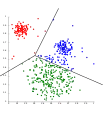 K-means rozdeľujúci dáta do Voronoiových buniek.
K-means rozdeľujúci dáta do Voronoiových buniek.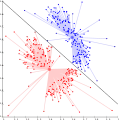 K-means nemôže reprezentovať zhluky na základe hustoty.
K-means nemôže reprezentovať zhluky na základe hustoty.
Zhlukovanie na základe distribúcie
Model zhlukovania, ktorý sa najviac blíži ku štatistike je založený na modeloch distribúcie. Zhluky možno potom ľahko definovať ako objekty, ktoré s najväčšou pravdepodobnosťou patria rovnakej distribúcii. Charakteristika tohto prístupu je, že sa veľmi podobá spôsobu generovania umelých dátových súborov: vzorkovaním náhodných súborov z distribúcie.
Kým teoretický základ týchto metód je vynikajúci, trpia kľúčovým problémom nazývaným „preučenie“, v prípade ak obmedzenia sú uložené na zložitosti modelu. Zložitejší model zvyčajne dokáže vysvetliť dáta lepšie, čo robí výber vhodného modelu zložitosti samo o sebe ťažké. Jedna prominentná metóda je známa ako zmes Gaussových modelov (pomocou algoritmu očakávaného maxima). Tu je dátový súbor zvyčajne modelovaný s pevným (aby sa zabránilo preučeniu) počtom Gaussových rozdelení, ktoré sú inicializované náhodne a sú optimalizované tak aby sa lepšie zmestili do dátového súboru. Tým sa približujú miestnemu optimu, takže viac spustení môže produkovať rôzne výsledky. V prípade ťažkého zhlukovania sú potom objekty priradené Gaussovému rozdeleniu, ku ktorému s najväčšou pravdepodobnosťou patria, pri ľahkom zhlukovaní to nie je nutné.
Zhlukovanie založené na distribúcii je sémanticky silná metóda, pretože nielen že poskytuje zhluky, ale taktiež pre nich vytvára zložité modely, ktoré môžu zachytiť vzťah a závislosti atribútov. Ale, použitie týchto algoritmov predstavuje ďalšiu záťaž pre užívateľa: voliť vhodné dátové modely pre optimalizáciu a pre m oho reálnych dátových súborov, pričom nemusí existovať matematický model, ktorý dokáže algoritmus optimalizovať (napríklad za predpokladu, že Gaussove rozdelenie je pomerne silný predpoklad pre dáta).
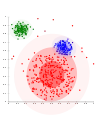 Na dátach Gaussovho rozdelenia pracuje EM dobre.
Na dátach Gaussovho rozdelenia pracuje EM dobre.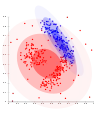 Zhluky na báze hustoty nemôžu byť modelované pomocou G. rozdelenia.
Zhluky na báze hustoty nemôžu byť modelované pomocou G. rozdelenia.
Zhlukovanie na báze hustoty [5]
Zhluky sú definované ako oblasti s vyššou hustotou, ako má zvyšok súboru dát. Objekty v týchto riedkych oblastiach – ktoré sú nutné na oddelenie zhlukov – sú zvyčajne považované za šum alebo hraničné body.
Najobľúbenejšia[6] metóda tohto zhlukovania je DBSCAN *. Na rozdiel od mnohých novších metód je vybavený dobre definovaným modelom zhlukov s názvom „hustota-dosiahnuteľnosť“. Podobne ako pri väzbovom zhlukovaní je založený na prepojení bodov v určitej vzdialenosti prahov. Ale, to len spája body, ktoré spĺňajú kritéria hustoty, v pôvodnej variante je definovaná ako minimálny počet ďalších objektov v rámci tohto okruhu. Zhluk sa skladá zo všetkých objektov pripojených na danú skupinu (ktoré môžu tvoriť zhluk ľubovoľného tvaru, na rozdiel od mnohých iných metód), zvýšenú o všetky objekty, ktoré sú v dosahu týchto objektov. Ďalšia zaujímavá vlastnosť DBSCAN je, že jeho zložitosť je pomerne nízka – to vyžaduje lineárny rad rozsahu otázok na databázu – a že objavuje v podstate rovnaké výsledky (je deterministický v jadre a na bodoch šumu, ale nie na hraničných prechodoch) v každom behu, a preto nie je potrebné ho spustiť viackrát. OPTICS * je zovšeobecnenie DBSCAN, ktoré odstraňuje nutnosť zvoliť vhodnú hodnotu pre rozsah parametra Ԑ, a vytvára hierarchický výsledok vzťahujúci sa k väzbovému zhlukovaniu. DeLiClu (Density-Link Clustering)* kombinuje nápady z jednoväzbového zhlukovania a OPTICS, čo eliminuje Ԑ parameter úplne a ponúka lepší výkon ako OPTICS pomocou R-tree index.
Kľúčovým nedostatkom DeLiClu a OPTICS je, že očakávajú pokles hustoty pre odhalenie hraníc zhluku. Okrem toho nemôžu detegovať vnútorné štruktúry zhluku, ktoré sú prevládajúce vo väčšine reálnych dát. Variácie DBSCAN a EnDBSCAN účinne detegujú tieto štruktúry. Na dátových súboroch s, napríklad prekrývajúcou sa Gaussovou distribúciou – spoločný prípad použitia v umelých dátach – hranice zhluku produkované týmito algoritmami vyzerajú často náhodne, pretože hustota zhluku klesá nepretržite. Na množine dát pozostávajúcich zo zmesí gaussovských distribúcií sú tieto algoritmy takmer vždy prekonané metódami, ako je EM zhlukovanie, ktoré sú schopné presne modelovať tento druh dát.
 Zhlukovanie na základe hustoty-DBSCAN.
Zhlukovanie na základe hustoty-DBSCAN.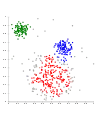 DBSCAN predpokladá zhluky podobnej hustoty.
DBSCAN predpokladá zhluky podobnej hustoty.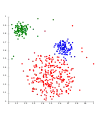 OPTICS spracováva hustoty lepšie.
OPTICS spracováva hustoty lepšie.
Posledný vývoj
V posledných rokoch bolo vyvinuté značné úsilie do vylepšenia výkonu existujúcich algoritmov.[7][8] Medzi nimi sú CLARANS (Ng a Han, 1994)[9] a BIRCH (Zhang et al., 1996)[10]. V súvislosti s potrebou spracovávať čoraz väčšie a väčšie dátové súbory ochota nahradiť sémantický význam výkonom stále rastie. To viedlo k vývoju pre-clustering metód ako napríklad canopy clustering, ktorý môže spracovávať veľké súbory dát efektívne, ale výsledky sú len hrubé pred-čistenie dát, ktoré sa potom musia ďalej rozdeliť do zhlukov pomalším algoritmom ako napríklad k-means *
Pre mnoho dimenzionálne dáta, mnoho z existujúcich metód zlyhali kvôli „prekliatiu rozmernosti“, ktorá činí funkcie vzdialenosti problematické v mnoho dimenzionálnom priestore. To viedlo k novým algoritmom zhlukovania pre mnoho dimenzionálne dáta, ktoré sa zameriavajú na pod-priestor zhlukovania a korelačné zoskupovanie, ktorý tiež hľadá ľubovoľne otočené pod-priestorové zhluky, ktoré možno modelovať pridávaním korelácie ich vlastností. Príklady takýchto zhlukovacích algoritmov sú CLIQUE * a SUBCLU[11].
Nápady zo zhlukovania na základe hustoty (najmä DBSCAN a OPTICS) boli prijaté podpriestorovým zhlukovaním (HiSC a DiSH) a korelačným zhlukovaním (HiCO, 4C a ERiC).
Bolo navrhnutých niekoľko rôznych zhlukovacích systémov založených na vzájomnej výmene informácií. Použitím genetických algoritmov môže byť široká škála rôznych funkcií optimalizovaná, vrátane vzájomnej výmeny informácií. Nedávny vývoj v oblasti výpočtovej techniky a štatistickej fyziky viedol k vytvoreniu nových typov zhlukovacích algoritmov.
Referencie
- Peter Sinčák, Gabriela Andrejková. Neurónové siete Inžiniersky prístup(1. diel). Kohonenové siete, s. 93-98. Dostupné online.
- Estivill-Castro, Vladimir. Why so many clustering algorithms — A Position Paper. ACM SIGKDD Explorations Newsletter, June 2002 2002, s. 65 – 75. Dostupné online. DOI: 10.1145/568574.568575.
- R. Sibson. SLINK: an optimally efficient algorithm for the single-link cluster method. The Computer Journal (British Computer Society), 1973, s. 30 – 34. Dostupné online. DOI: 10.1093/comjnl/16.1.30.
- D. Defays. An efficient algorithm for a complete link method. The Computer Journal (British Computer Society), 1977, s. 364 – 366. DOI: 10.1093/comjnl/20.4.364.
- Hans-Peter Kriegel, Peer Kröger, Jörg Sander, Arthur Zimek. Density-based Clustering. WIREs Data Mining and Knowledge Discovery, 2011, s. 231 – 240. Dostupné online. DOI: 10.1002/widm.30.
- Microsoft academic search: most cited data mining articles: DBSCAN is on rank 24, when accessed on: 4/18/2010
- D. Sculley (2010). "Web-scale k-means clustering". Proc. 19th WWW.
- Z. Huang. "Extensions to the k-means algorithm for clustering large data sets with categorical values". Data Mining and Knowledge Discovery, 2:283 – 304, 1998.
- R. Ng and J. Han. "Efficient and effective clustering method for spatial data mining". In: Proceedings of the 20th VLDB Conference, pages 144 – 155, Santiago, Chile, 1994.
- Tian Zhang, Raghu Ramakrishnan, Miron Livny. "An Efficient Data Clustering Method for Very Large Databases." In: Proc. Int'l Conf. on Management of Data, ACM SIGMOD, pp. 103 – 114.
- Karin Kailing, Hans-Peter Kriegel and Peer Kröger. Density-Connected Subspace Clustering for High-Dimensional Data. In: Proc. SIAM Int. Conf. on Data Mining (SDM'04), pp. 246 – 257, 2004.