Binárna sčítačka
Binárna sčítačka (alebo len sčítačka) je kombinačný logický obvod, realizujúci sčítanie čísel, reprezentovaných v binárnej číselnej sústave. Tvorí dôležitú súčasť aritmeticko-logickej jednotky (ALU) centrálneho procesora (CPU) počítača.
V prípade použitia dvojkového doplnkového kódovania záporných čísel sa dá sčítačka veľmi jednoducho rozšíriť na sčítačku-odčítačku.
Jednobitové sčítačky
Polovičná sčítačka
Polovičná sčítačka (angl. Half adder) realizuje sčítanie dvoch jednomiestnych binárnych čísel. Vstupom sú dva jednobitové sčítance (A, B). Výstupom je jednobitový súčet (S) a jednobitový príznak prenosu do vyššieho rádu (C, z angl. Carry flag).
Polovičná sčítačka odovzdáva ďalej príznak prenosu do ďalšieho rádu, sama však nedokáže spracovať prenos z predchádzajúceho rádu. Nestačí preto na realizáciu viacbitového sčítania.
Booleovský zápis:
Pravdivostná tabuľka polovičnej sčítačky:
| vstup | výstup | |||
|---|---|---|---|---|
| A | B | C | S | |
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 0 | |
Úplná sčítačka
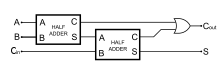

Úplná sčítačka (angl. Full adder) realizuje sčítanie dvoch jednomiestnych binárnych čísel s pripočítaním prenosu z predchádzajúceho rádu. Vstupom sú tri jednobitové sčítance: A, B, Ci (Ci z angl. Carry-in). Výstupom je jednobitový súčet (S) a jednobitový príznak prenosu do vyššieho rádu (Co, z angl. Carry-out).
Úplnú sčítačku je možné zložiť z dvoch polovičných sčítačiek a hradla OR (pozri obr.). Hradlo OR je navyše možné bez vplyvu na funkčnosť nahradiť hradlom XOR, nakoľko kombinácia vstupov (1, 1), pri ktorej by sa ich výstup líšil nemôže v prípade sčítania nastať (buď nastane prenos iba v prvej polovičnej sčítačke, alebo iba v druhej). Na vytvorenie úplnej sčítačky tak stačia 2 typy hradiel, čo je praktické pri ich realizácii.
Úplné sčítačky je možné zreťaziť vedľa seba (výstup Co jednej sčítačky prepojiť so vstupom Ci ďalšej) a realizovať tak sčítanie viacbitových čísel (pozri nižšie).
Booleovský zápis:
Pravdivostná tabuľka úplnej sčítačky:
| vstup | výstup | ||||
|---|---|---|---|---|---|
| A | B | Ci | Co | S | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | |
Viacbitové sčítačky
Sčítačka s propagáciou prenosu

N-bitová sčítačka s propagáciou prenosu (angl. Ripple carry adder, skr. RCA) vznikne jednoduchým zreťazením N úplných 1-bitových sčítačiek, prepojením výstupu Co úplnej sčítačky n-tého bitu so vstupom Ci sčítačky (n+1). bitu (pozri obr.). Vstupom výslednej N-bitovej sčítačky sú potom dve N-bitové čísla (+ prípadný prenos z predchádzajúceho rádu), výstupom je ich súčet, široký N+1 bitov (N bitov + prenos). Názov je odvodený z princípu – príznak prenosu sa odovzdáva (propaguje) z jedného bitu do druhého.
Sčítačka s propagáciou prenosu je jednoduchá na návrh a realizáciu a teoreticky je rozšíriteľná na ľubovoľný počet bitov. Má však zásadnú nevýhodu: s rastúcou šírkou (a teda počtom zreťazených úplných sčítačiek) priamo úmerne narastá celkové oneskorenie (doba ustálenia) výsledného obvodu. Signál prenosu prechádza v každej úplnej sčítačke dvoma hradlami, takže korektný súčet sa na výstupe napr. 32-bitovej sčítačky s propagáciou prenosu objaví s oneskorením až 64 čiastkových hradlových oneskorení, čo by mohlo výrazne obmedzovať priepustnosť (maximálny možný počet sčítaní za jednotku času) sekvenčného zariadenia, využívajúceho takýto typ sčítačky. Toto obmedzenie viedlo k snahe navrhnúť N-bitové sčítačky s menším oneskorením.
Sčítačka s predikciou prenosu
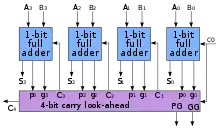
Sčítačka s predikciou prenosu (angl. Carry Lookahead Adder, skr. CLA) je N-bitová binárna sčítačka, schopná vypočítať súčet v kratšom čase (v jednotkách hradlového oneskorenia) než sčítačka s propagáciou prenosu (RCA). Pri RCA musí každá čiastková 1-bitová sčítačka „čakať“ na korektný príznak prenosu od sčítačky predchádzajúceho bitu. Pri CLA sú (zjednodušene povedané) všetky prenosy medzi rádmi vypočítané súčasne – kombinačným obvodom, nazývaným jednotka predikcie prenosu (angl. Lookahead Carry Unit, skr. LCU).
Výhody:
- výpočet súčtu s oneskorením, teoreticky nezávislým od šírky vstupu – O(), zatiaľ čo sčítačka s propagáciou prenosu má oneskorenie priamo úmerné šírke vstupu – O()
Nevýhody:
- vyššie nároky na celkový počet hradiel – O() a celkový počet tranzistorov (O() kvôli potrebe hradiel s počtom vstupov úmerným šírke sčítačky) v porovnaní so sčítačkou s propagáciou prenosu (O() hradiel)
- od určitého počtu bitov prestáva byť prakticky realizovateľná (kvôli počtu hradiel a výrobným obmedzeniam na počet vstupov jedného hradla). Široké sčítačky je preto potrebné realizovať viacúrovňovo – kombinovaním princípu predikcie prenosu (na nižšej úrovni) s propagáciou prenosu (na vyššej úrovni), prípadne použitím princípu predikcie prenosu na dvoch (alebo viacerých) úrovniach.
Pozri aj
- Binárna násobička
- Aritmeticko-logická jednotka (ALU)
- Hradlo XOR
- Zoznam základných logických obvodov

