Radix sort
Radix sort je v informatike triediaci algoritmus, ktorý triedi celé čísla spracovaním jednotlivých čísel, porovnaním jednotlivých číslic zdieľajúcich rovnaké významné postavenie. Pozičné číselná sústava je potrebná, ale preto, že celé čísla môžu reprezentovať reťazce znakov (napr., mena alebo dátumu) a špeciálne formátované desatinné čísla, radix sort nie je obmedzený iba na celé čísla. História radix sortu siaha až do roku 1887 k práci Hermana Holleritha na zostavovanie tabuľkových strojov[1].
Väčšina digitálnych počítačov vnútorne reprezentovalo všetky ich dáta v elektronickej reprezentácii binárnych čísiel, takže spracovanie reprezentácie celých čísel podľa skupín reprezentácie binárnych číslic je najvhodnejší. Dve klasifikácie radix sortu sú least significant digit (LSD) a most significant digit (MSD). LSD radix sort spracúva integer reprezentácie od najmenej významných číslic a približuje sa k najvýznamnejším čísliciam. MSD radix sort pracuje naopak.
Celočíselné reprezentácie, ktoré sú spracované triediacimi algoritmami sú často nazývané „kľúče“, ktoré sa môžu vyskytovať všetky samé o sebe alebo byť spojené s inými údajmi. LSD radix sort zvyčajne používa nasledujúce radenie: krátke kľúče prv, než dlhšie , a kľúče rovnakej dĺžky, sú zoradené lexikograficky. To sa zhoduje s normálnym poradím integer reprezentácie, ako poradie 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. MSD radix sort používa lexikografické poradie, ktoré je vhodné pre triedenie reťazcov, ako sú slová, alebo integer pevnej dĺžky. Sekvencie, ako je "b, c, d, e, f, g, h, i, j, ba" by lexikograficky zoradil na "b, ba, c, d, e, f, g, h, i, j ". Ak lexikografické usporiadanie slúži na radenie integerov premennej dĺžky, potom reprezentácia čísel od 1 do 10 by mala výstup 1, 10, 2, 3, 4, 5, 6, 7, 8, 9, ako keby kratšie kľúče boli zarovnané vľavo a doplnené sprava s prázdnymi znakmi tak, aby kratšie kľúče mali dĺžku ako najdlhší kľúč pre účel určovania utriedeného poradia.
Príklad
Táto metóda triedi postupnosť K-miestnych čísel dĺžky N a pracuje na princípe priehradkového zariadenia. Vyrobí sa desať priehradiek pomocou dátovej štruktúry rad (FIFO - z anglického First-In-First-Out.) pre každú číslicu z intervalu 0 až 9. Vlastné triedenie prebieha takto: V prvom prechode vstupnej postupností čísel zaraďujeme do vzniknutých priehradiek podľa ich posledných číslic (jednotky), potom čísla z priehradiek spojíme do novej postupnosti. V ďalšom prechode čísla z tejto novej postupnosti zaraďujeme do vzniknutých priehradiek podla ich predošlej číslice (desiatky), potom čísla spojíme do ďalšej novej postupnosti. Takto rozdeľujeme a spájame po jednotlivých riadkoch číslic až do riadku K. Celý postup si je možné ukázať na obrázku, kde budeme triediť dvojciferné čísla.[2]

Postupnosť výberu cifier.
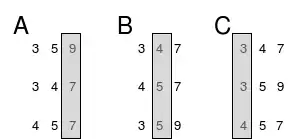
Zložitosť
Myšlienka algoritmu Radix sort spočíva v rozdeľovaní do tried, ktoré prebieha so zložitosťou O(n) v každom ráde. To znamená, že celková zložitosť algoritmu je O(D*n) , kde D je dĺžka radených prvkov. Keby sme D považovali za konštantu, operačná zložitosť Radix sortu by bola O(n) .
Ak by bolo možné, aby D narastalo spolu s n, potom D = log n a dostaneme :
= O(n*log n + 2*log n) = O(n*log n)
kde s je počet skupín.
Zložitosť Radix sort je teda O(n*log n)[3]
Implementácia
Java
import java.util.*;
public class radixSort {
public static int[] spracuj(int[] cisla,int max,int miesto){
int[] pom=new int[cisla.length];
pom=usortuj(cisla, max, miesto);
if(miesto==0)
return pom;
else
return spracuj(pom, max,miesto-1);
}
public static int pocetMocnin(int cislo){
int pocet=0;
do{
cislo=cislo/10;
pocet++;
}while(cislo!=0);
return pocet;
}
public static int najdlhsie(int[] cisla){
int max=0;
for(int i=0;i<cisla.length;i++)
max=Math.max(max, pocetMocnin(cisla[i]));
return max;
}
public static int mocnina(int x){
int mocnina=1;
for(int i=1;i<x+1;i++)
mocnina=mocnina*10;
return mocnina;
}
public static int[] usortuj(int[] cisla,int max,int miesto){
Queue<Integer>[] p = new Queue[10];
int[] pom=new int[cisla.length];
for (int i=0; i<10; i++)
p[i] = new LinkedList<Integer>();
for(int i=0;i<cisla.length;i++){
p[(cisla[i]/(mocnina(max-miesto)))%10].add( cisla[i]);
}
int x=0;
for(int i=0;i<p.length;i++){
while(p[i].size()!=0){
pom[x]=p[i].poll();
x++;
}
}
return pom;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println("koľko chceš zadať čísel?");
Scanner sc= new Scanner(System.in);
int pocet=sc.nextInt();
int[] cisla=new int[pocet];
for(int i=0;i<pocet;i++){
System.out.println("zadaj "+(i+1)+". číslo");
cisla[i]=sc.nextInt();
}
int max=najdlhsie(cisla);
int[] usortovane=new int[pocet];
usortovane=spracuj(cisla,max,max);
System.out.println("radixsortom usporiadané;");
for(int i=0;i<pocet;i++)
System.out.println(" "+usortovane[i]);;
}
}
Vstup: počet zadaných čísel+ čísla, ktoré chceme usortovať
Vystúp: čísla zoradené pomocou radix sortu
Referencie
Externé odkazy
- Bakalářská práce popisující Algoritmy číslicového třídění(CZ), součástí práce je i měření výkonu algoritmů, kódy algoritmů v jazyce C# a studijní aplikace.