Kirchhoffove zákony
Kirchhoffove zákony sú dve pravidlá stanovujúce princípy zachovania náboja a energie v elektrických obvodoch. Sú jedným zo základných nástrojov pri teoretickej analýze obvodov. Zákony boli pomenované podľa ich objaviteľa Gustava Roberta Kirchhoffa, ktorý ich prvýkrát opísal roku 1845. Využívajú sa pri riešení elektrických obvodov.

i1 + i4 = i2 + i3
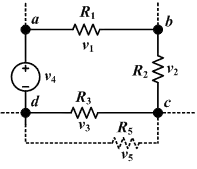
v1 + v2 + v3 + v4 = 0
Oba zákony možno priamo odvodiť z Maxwellových rovníc, ktoré však boli formulované až v roku 1864; Kirchhoff zákony vytvoril ako zovšeobecnenie výsledkov Georga Ohma.
Okrem Kirchhoffových zákonov pre elektrické obvody existuje aj Kirchhoffov zákon tepelného vyžarovania a ďalšie empirické Kirchhoffove zákony opisujúce vyžarovacie spektrá.
Prvý Kirchhoffov zákon (o prúdoch, o uzloch)
Prvý Kirchhoffov zákon opisuje zákon zachovania elektrického náboja; hovorí, že v každom bode (uzle) elektrického obvodu platí, že:
- Súčet prúdov vstupujúcich do uzla sa rovná súčtu prúdov z uzla vystupujúcich.
alebo
- Algebrický súčet prúdov v ktoromkoľvek uzle elektrického obvodu sa rovná nule.
Druhý Kirchhoffov zákon (o napätí, o slučkách)
Druhý Kirchoffov zákon formuluje pre elektrické obvody zákon zachovania energie; hovorí, že:
- Súčet úbytkov napätia na spotrebičoch sa v uzavretej časti obvodu (slučke) rovná súčtu elektromotorických napätí zdrojov v tejto časti obvodu.
alebo
- Súčet svorkových napätí prvkov elektrického obvodu v ľubovoľnej slučke sa rovná nule.
Ak by zákon pre nejakú slučku neplatil, mohlo by byť konštruované Perpetuum mobile, v ktorom by prúd touto slučkou prechádzal neustále dokola pri permanentnom odbere energie.
Použitie Kirchhoffových zákonov
Kirchhoffove zákony sa používajú najmä pre rozvetvené elektrické obvody, pretože spolu s Ohmovým zákonom umožňujú určiť veľkosť a smer elektrického prúdu v jednotlivých vetvách a veľkosť elektrického napätia na svorkách jednotlivých prvkov.
Pri analýze obvodu pomocou Kirchhoffových zákonov je možné použiť jednu z dvoch metód: analýzy uzlov (založené na použití 1. Kirchoffovho zákona) alebo analýzu slučiek (založenú na použití 2. Kirchhoffovho zákona).
Metóda uzlov
- V obvode sa nájdu a označia všetky uzly.
- Ľubovoľne zvolenému uzlu sa priradí nulový elektrický potenciál.
- Všetkým zostávajúcim sa priradí neznáme napätie oproti referenčnému uzlu.
- Pre každý z uzlov okrem referenčného sa zostaví rovnica podľa 1. Kirchhoffovho zákona.
- Táto sústava rovníc sa potom vyrieši.
Metóda slučiek
- Na diagrame sa nájdu elementárne slučky, tzn. slučky, ktoré neobsahujú menšie vnorené slučky.
- Každej takejto slučke sa priradí prúd, ktorý v nej obieha.
- Pre každú slučku sa zapíše rovnica podľa 2. Kirchhoffovho zákona, v ktorej sa ako neznáma použije prúd pretekajúci slučkou.
- Táto sústava rovníc sa potom vyrieši.
Voľba metódy
Obe metódy poskytujú rovnaké výsledky, pre daný obvod však môže byť jedna alebo druhá metóda jednoduchšia. Metódy vyžadujú riešenie sústavy n rovníc o n neznámych. U metódy uzlov je n počet uzlov mínus počet všetkých zdrojov napätia mínus jedna (za referenčný uzol). U metódy slučiek je n rovné počtu elementárnych slučiek mínus počet zdrojov prúdu. Zvyčajne sa preto používa tá metóda, ktorá si vyžaduje riešenia menšieho počtu rovníc.
Je však potrebné poznamenať, že metódu slučiek možno použiť len pre planárne obvody, teda obvody, na ktorých schéme sa nekrižujú vodiče. Taká je ale väčšina obvodov, ktoré sa v praxi vyskytujú.
Kirchhoffove zákony v striedavých obvodoch
Analýzu pomocou Kirchoffových zákonov možno vykonávať v obvodoch jednosmerného prúdu, ako aj v obvodoch striedavého prúdu. V tých sa napätie a prúd vyjadrujú komplexnými číslami, ktoré reprezentujú fázory, a miesto elektrického odporu sa používa impedancia.
Kirchhoffove zákony v teórii grafov
Kirchhoffove zákony sa okrem elektroinžinierstva používajú aj v teórii grafov pre analýzy tokov (ktoré sú všeobecné zavedenie elektrického prúdu) v sieťach (ktoré sú všeobecné zavedenie schémy elektrického obvodu). Dokonca sa dá povedať, že teória grafov ako taká má v Kirchhoffových zákonoch svoje korene.
Zdroj
Tento článok je čiastočný alebo úplný preklad článku Kirchhoffovy zákony na českej Wikipédii (číslo revízie nebolo určené).