Bernoulliho rovnica

Bernoulliho rovnica je dôležitý vzťah používaný v hydrodynamike, ktorý je matematickým vyjadrením zákona zachovania energie v ustálenom toku kvapaliny alebo plynu. Zákon odvodil švajčiarsky matematik Daniel Bernoulli.

Obr. 1.a Prúdová trubica s naznačenými prúdnicami

Obr. 1.b Pohyb tekutiny v prúdovej trubici

Odvodenie

Jedno z možných odvodení Bernoulliho rovnice vychádza zo zákona zachovania energie v kvapaline. Pri odvádzaní sa využíva predpoklad ustálenosti prúdenia, t. j. že na žiadnom mieste tekutiny sa rýchlosť nemení s časom.

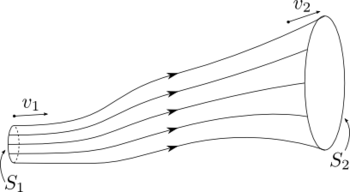
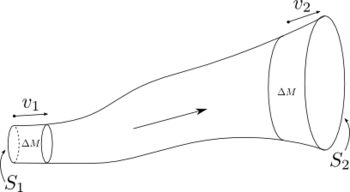
Predstavme si zväzok blízkych prúdnic, ktoré formujú prúdovú trubicu ako na obr. 1a. Keďže steny trubice sú tvorené prúdnicami, nevyteká nimi žiadna tekutina. Označme plochu prierezu na vtoku do trubice $S_{1}$ , rýchlosť tekutiny v tomto bode označme $v_{1}$ . Obdobne označme plochu prierezu a rýchlosť tekutiny na výtoku ako $S_{2}$ a $v_{2}$ . Keďže prúdenie je ustálené, v trubici sa nemôže hromadiť tekutina. To znamená, že hmotnosť vytečenej a vtečenej tekutiny za jednotku času musí byť rovnaká:

\Delta M=\rho _{1}S_{1}v_{1}\Delta t=\rho _{2}S_{2}v_{2}\Delta t

Máme teda rovnosť:

\rho _{1}S_{1}v_{1}=\rho _{2}S_{2}v_{2}

Tiež známu ako rovnicu kontinuity.

Teraz vypočítame prácu, ktorú vykonal tlak v tekutine. Práca vykonaná na tekutine, ktorá vteká do $S_{1}$ je $p_{1}S_{1}v_{1}\Delta t$ zatiaľ čo práca odovzdaná na výtoku je $p_{2}S_{2}v_{2}\Delta t$ . Výsledná práca vykonaná na tekutine medzi $S_{1}$ a $S_{2}$ je preto:

p_{1}S_{1}v_{1}\Delta t-p_{2}S_{2}v_{2}\Delta t

a musí byť rovná zvýšeniu energie tekutiny hmotnosti $\Delta M$ pri prechode z $S_{1}$ do $S_{2}$ . Teda:

p_{1}S_{1}v_{1}\Delta t-p_{2}S_{2}v_{2}\Delta t=\Delta M(E_{2}-E_{1})

pričom $E_{1}$ je energia na jednotku hmotnosti tekutiny na vtoku a $E_{2}$ na výtoku. Energiu na jednotku hmotnosti môžeme zapísať ako:

E={\frac {1}{2}}v^{2}+\varphi +W

Kde ${\frac {1}{2}}v^{2}$ je kinetická energia na jednotku hmotnosti, $\varphi$ je potenciálna energia na jednotku hmotnosti a $W$ je člen, ktorý reprezentuje vnútornú energiu jednotky hmotnosti tekutiny. Dosadením vzťahu do predchádzajucej rovnice potom dostávame:

{\frac {p_{1}S_{1}v_{1}\Delta t-p_{2}S_{2}v_{2}\Delta t}{\Delta M}}={\frac {1}{2}}v_{2}^{2}+\varphi _{2}+W_{2}-{\frac {1}{2}}v_{1}^{2}-\varphi _{1}-W_{1}

Keďže však $\Delta M=\rho Sv\Delta t$ , tak dostaneme výraz:

{\frac {p_{1}}{\rho _{1}}}+{\frac {1}{2}}v_{1}^{2}+\varphi _{1}+W_{1}={\frac {p_{2}}{\rho _{2}}}+{\frac {1}{2}}v_{2}^{2}+\varphi _{2}+W_{2}

známy tiež ako Bernoulliho rovnica.

Bernoulliho rovnica pre ideálnu kvapalinu

Ideálna kvapalina je nestlačiteľná a neviskózna, preto je vnútorná energia na oboch stranách rovnice rovnaká a možno ju od oboch strán odčítať. Rovnako je rovnaká hustota, ktorá sa z premenej stane konštantou. Po úprave:

{\frac {p_{1}}{\rho }}+{\frac {1}{2}}v_{1}^{2}+\varphi _{1}={\frac {p_{2}}{\rho }}+{\frac {1}{2}}v_{2}^{2}+\varphi _{2}

Vymedzenie platnosti

Vyššie uvedená rovnica platí len pre nasledovné prípady[1]:

stále sa uvažuje ustálené prúdenie tekutiny
ide o niektorú z nasledovných geometrických podmienok:
- nevírivé prúdenie kvapaliny – v tomto prípade je rovnica platná pre celý rozsah prúdu, pretože súčet všetkých členov jednej strany je konštantný v ľubovoľnom bode celého priestoru prúdiacej tekutiny.
- vírivé prúdenie po prúdnici – rovnica platí len pre jednotlivú prúdnicu, súčet členov pre rôzne prúdnice nie je rovnaký.
- vírivé prúdenie po vírovej čiare – rovnica platí len pre jednotlivú vírovú čiaru, súčet členov pre rôzne vírové čiary nie je rovnaký.
- skrutkový pohyb kvapaliny – je to pohyb pri ktorom je každá prúdnica totožná s nejakou vírovou čiarou. častice kvapaliny teda prúdia po prúdnici a pritom sa okolo nej otáčajú. V tomto prípade je rovnica platná pre celý rozsah prúdu, pretože súčet členov v ľubovoľnom bode celého priestoru prúdu je konštantný.

Prúdenie v gravitačnom poli

Pre špecifický (a prakticky najužitočnejší) prípad prúdenia v gravitačnom poli zeme sa člen potenciálnej energie na jednotku hmotnosti môže nahradiť vzťahom $\varphi =gh\$ Potom je platí:

{\frac {p_{1}}{\rho }}+{\frac {1}{2}}v_{1}^{2}+gh_{1}={\frac {p_{2}}{\rho }}+{\frac {1}{2}}v_{2}^{2}+gh_{2}

Táto, ako aj všetky vyššie uvedené rovnice sú vo forme špecifických energií. Každý člen, ako aj súčet má rozmer J.kg⁻¹.

Iné formy rovnice

Pre praktické účely sa využívajú aj iné formy vyjadrenia Bernoulliho rovnice: Po vydelení základnej formy gravitačným zrýchlením je rovnica v tvare výšok s rozmerom každého člena v m:

{\frac {p_{1}}{\rho g}}+{\frac {v_{1}^{2}}{2g}}+h_{1}={\frac {p_{2}}{\rho g}}+{\frac {v_{2}^{2}}{2g}}+h_{2}

kde jednotlivé čeny v uvedenom poradí sa nazývajú:

tlaková výška
rýchlostná výška
výška (polohová výška)

Po vynásobení základnej formy hustotou je rovnica v tvare tlakov s rozmerom každého člena v Pa:

p_{1}+{\frac {v_{1}^{2}\rho }{2}}+\rho gh_{1}=p_{2}+{\frac {v_{2}^{2}\rho }{2}}+\rho gh_{2}

kde jednotlivé čeny v uvedenom poradí sa nazývajú:

tlak
dynamický tlak
hydrostatický tlak

Zjednodušená Bernoulliho rovnica

Ak kvapalina neprekonáva žiaden potenciálový rozdiel, rovnica sa zjednoduší do známejšieho tvaru:

p_{1}+{\frac {1}{2}}\rho v_{1}^{2}=p_{2}+{\frac {1}{2}}\rho v_{2}^{2}

Ktorý hovorí, že súčet hustoty kinetickej energie kvapaliny a jej tlaku je v každom bode prúdnice rovnaký.

ρ – hustota kvapaliny
p – tlak v kvapaline
v – rýchlosť prúdenia kvapaliny

Z tejto rovnice vyplýva, že čím je rýchlosť prúdenia kvapaliny vyššia, tým je tlak v nej nižší (Venturiho efekt).

Názvoslovie členov v Bernoulliho rovnici

V zjednodušenej Bernoulliho rovnici:

p_{1}+{\frac {1}{2}}\rho v_{1}^{2}=p_{2}+{\frac {1}{2}}\rho v_{2}^{2}

Vyjadruje prvý člen prácu vykonanú na kvapaline a druhý člen jej kinetickú energiu. Z tohto dôvodu sa občas prvý člen zvykne nazývať hustotou tlakovej práce, často sa však stretneme aj s pojmom hustota tlakovej energie. Je dôležité upozorniť, že nejde o energiu v pravom slova zmysle, ale člen svoj názov pravdepodobne dostal preto, že má rozmer hustoty energie. Niektorí autori preto odporúčajú vyvarovať sa používaniu mätúceho, ale zaužívaneho, pojmu hustota tlakovej energie a hovoriť miesto toho o hustote tlakovej práce

Zdroje

Feynmanove prednášky z Fyziky, druhý diel (ISBN 80-7200-420-4)

Referencie

Gančo Martin: Mechanika tekutín. 2. vydanie. Bratislava, Alfa. 1990 (SVŠT SjF)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Gančo-1] Gančo Martin: Mechanika tekutín. 2. vydanie. Bratislava, Alfa. 1990 (SVŠT SjF)