Vágnost

O svých inherentně vágních poznatcích (vnitropsychickém kognitivním modelu reprezentovaném v hypotetických vnitropsychických jazycích) je člověk schopen vypovídat přirozeným (obecně neformálním jazykem, např. esperanto) a to samozřejmě pouze vágně[1]. Vágnost znalostí zapříčiněná filtrem poznání je primární, říkáme jí vnitřní. Vágnost následné výpovědi člověka je sekundární. Touto výpovědí (transformací z vnitropsychických jazyků do vnějšího komunikačního - říká se jí formulace, viz konotace a tam sémantický trojúhelník) nelze odkrýt veškerý obsah osobního vnitropsychického kognitivního modelu s veškerou jeho inherentní vágností. Tu, která je obsažena v jazykové výpovědi, označujeme jako vnější vágnost[2],[3],[4]. Pokud by člověk neměl schopnost sdělovat a ponechával by si tak veškeré své znalosti pouze pro sebe, vnější vágnost by neexistovala, neboť je to vágnost vnějšího sdělovacího jazyka.

Vnitřní vágnost sdělení jednoho člověka je pro druhého člověka utajená, může jí jen tušit, odhadovat. S vnitřní vágností (v interpretaci jazykové konstrukce, primárně tedy ve vnitropsychickém kognitivním modelu sdělujícího člověka – zdroje informace) se buď musíme smířit, což je lidské, nebo se můžeme pokusit ji zmenšovat, případně zcela odstranit, což je vědecké. Nároky na přesnost formulace vědeckých poznatků a jejich sdělování vyžadují minimalizovat vnitřní vágnost, s níž člověk konotuje (vágně, emocionálně a subjektivně interpretuje) jazykové konstrukce sdělovacího jazyka, a takto zlepšovat přesnost sdělení. Nejrůznější vědecké postupy mají za cíl zkvalitňovat důvěryhodnost a přesnost získaných vědeckých poznatků. Pro jejich formulaci je však třeba budovat přesnější jazyk, s menší vágností sdělení, než je běžné v denním životě. Slouží k tomu účelově (oborově) budovaná názvosloví umožňující přesněji popsat zkoumanou realitu a získané znalosti o ní. Lidé vzdělaní v oboru názvosloví znají s malou vnitřní vágností, tedy dost přesně vědí, co jednotlivé pojmy znamenají. Základní pojmy jsou vždy tvořeny na základě konsensu, odvozené z nich pak definicí. Ke zlepšení přesnosti bádání a sdělování (snižování vnitřní vágnosti konotace) slouží i nástroje typu klasifikačních schémat např. taxonomie organizmů, jejímž autorem je Carl von Linné.

Potřeba snížit vnitřní vágnost až do extrému, tedy nuly, byla uskutečněna I. Newtonem. Je to epochální myšlenka, a je třeba vysvětlit, jak může být uskutečněna. Z výše uvedené optimalizace pravdivosti sdělení plyne, že požadujeme-li odbourat vnitřní vágnost ve sdělení zcela (anulovat ji), pak ovšem musí být nejprve zcela odbourána v poznání (zdroji informace). Znamená to, že se musíme vyhnout vniku vnitřní vágnosti, tedy zvolit jiný filtr poznání, než je vágnost. Tím přecházíme z přirozeného lidského světa, do světa umělého. Říkáme mu svět exaktní, a vysvětlíme proč. U přirozeného jazyka nelze zcela odstranit (anulovat) vnitřní vágnost, lze však vybudovat umělé formální jazyky (matematika, formální logiky, programovací jazyky), které mají vnitřní vágnost konotace nulovou (tak mají exaktní interpretaci) a jinou mít z principu nemohou. A nyní slíbené vysvětlení. Jazyky s nulovou vnitřní vágností konotace, tedy významu svých jazykových konstrukcí, mají tu vlastnost, že veškeré tyto konstrukce jsou každým patřičně vzdělaným člověkem, chápány s naprosto přesným, tedy exaktním významem. To je důvod, proč jsou součástí exaktního světa. Máme tedy jazyk, který je schopen zapisovat (reprezentovat) znalosti s nulovou vnitřní vágností. Ty však nejdříve musí být získány odpovídajícím poznáním, poskytujícím znalosti rovněž s nulovou vnitřní vágností, tedy rovněž z exaktního světa. A již je zřejmé, že jsme na cestě zrodu vědecké metody tvořící vědu náležející do exaktního světa, tedy rodí se exaktní věda. Ještě je třeba vysvětlit, jak uskutečnit exaktní poznání, tedy poznání, kdy znalosti získané z reálného světa jsou součástí exaktního světa. Zázračný most mezi reálným a exaktním světem, který to umožňuje, se jmenuje veličina (např. intenzita elektrického pole, rychlost, koncentrace kyseliny dusičné, atp.). Je společná oběma zmíněným světům, neboť v exaktním světě je exaktně vytyčena (každý vědoucí člověk bez nejmenších pochyb ví, co znamená, tedy jaký má význam), a v reálném světě je elementární měřitelnou sondou do něho, a tak jeho elementárním měřitelným zástupcem. Je elementárním stavebním kamenem exaktní vědy. V exaktních vědách je vždy přesně vymezena a to buď konsensuálně (základní množina - Základní fyzikální veličiny), nebo definitoricky (odvozené - Odvozená jednotka SI). V tomto duchu píše I. Newton ve svém díle Philosophiae Naturalis Principia Mathematica v roce 1687. V současné době celosvětově zavedená soustavy veličin SI (z franc. Système international d'unités). A jak je to s tím umělým filtrem, který umožňuje vyhnout se vnitřní vágnosti? Pro každý problém reálného světa, který má být uchopen exaktní vědou, je třeba zvolit skupinu vhodných veličin, nalézt přírodní zákonitosti, které v reálném světě mezi nimi platí, a ty popsat matematickým jazykem. Dostáváme tak matematický znalostní (kognitivní) model dané části reálného světa. Skupina vybraných veličin tvoří diskrétní Newtonův filtr (síto), kterým se na danou část reálného světa díváme. Tak je v exaktní vědě daná část reálného světa zastoupena skupinou vhodně zvolených veličin a matematicky (programovacím jazykem) popsanými vztahy mezi nimi (přesněji mezi jejich jmény – symboly je označujícími). I exaktní věda musí mít nástroj, kterým může popsat neurčitost získaných výsledků - znalostí, ať už z nutnosti, či z potřeby opustit přílišnou přesnost. Jelikož vnitřní vágnost to být nemůže (nesmí), může použít pouze jazykově uchopitelnou nejistotu (vnější vágnost), a pro ten účel je k dispozici popis fuzzy nebo stochastickými hodnotami veličin, a fuzzy či stochastickými vztahy mezi veličinami.

Umělý formální jazyk přináší exaktní vědě ještě navíc silný nástroj (pro zpracování informace), kterým je formální odvozování (inference) známé z matematiky, viz Exaktní věda výklad a Příklad inference ve formálním systému. Exaktní věda poskytuje nedůvěryhodnější znalosti. Jistě je možno nastolit otázku, zda veškerá věda může být přetvořena na exaktní vědu. Odpověď je nemůže. Podmínkou pro ustavení exaktní vědy je nalezení vhodných veličin, a to lze jen pro nepatrnou část reálného světa a pro specifické pohledy na něj. Jinak řečeno, filtr vágnosti umožňuje vágně znát mnohé, diskrétní filtr umožňuje exaktně znát nemnohé. To z reálného světa, co umíme poznat exaktní vědou, tedy zavést veličiny a rozpoznané přírodní zákonitosti mezi nimi zapsat umělým formálním jazykem (matematika, formální logiky, programovací jazyky), jsme schopni modelovat na počítači.

Myšlenka vypořádat se s vnitřní vágností, je jistě pro vědu z hlediska poznání reálného světa přelomová. Též umožnila typologicky rozdělit nástroje na zpracování informace na lidský (lidskou psýchu), v němž je zpracovávaná informace inherentně svázaná se svojí (vnitřní) vágností a na umělý exaktní (matematika, formální logiky, programovací jazyky - tedy algoritmické zpracování) se zakázanou (nulovou) vnitřní vágností. Jsou to tedy z hlediska typu zpracovávané informace mimoběžné světy.

Jazykově lze uchopit (modelovat) pouze vágnost vnější. Vnitřní vágnost modelovat neumíme, je součástí vnitropsychického modelu. Neformální jazyky, např. přirozený jazyk, neumožňují rozlišit vnitřní a vnější vágnost striktně, ale pouze s mlhavou, vágní hranicí.[3],[4]. Naštěstí však tyto jazyky používají vhodné znejisťující a znepřesňující jazykové konstrukce (např. neurčité kvantifikátory ASI, NEJSPÍŠ, NĚKOLIK, MOŽNÁ atp.). Přirozenému jazyku takové kvantifikátory umožňují výrazněji a explicitněji používat vnější vágnost, a tak umožňují vnitřní vágnost částečně přesunout do vnější vágnosti. Je to cesta, jak adresáta na vágnost sdělení explicitněji upozorňovat a vágnost kvantifikovat, a zlepšovat tak porozumění v komunikaci přirozeným jazykem. Umělé formální jazyky (z principu musí mít nulovou vnitřní vágnost interpretace všech jazykových konstrukcí) mohou vnější vágnost modelovat fuzzy množinami[5] a fuzzy logikou[6], mírou důvěry[7], Bayesovou apriorní a aposteriorní pravděpodobností, nebo stochastickými veličinami a funkcemi, jak to činí exaktní vědy.

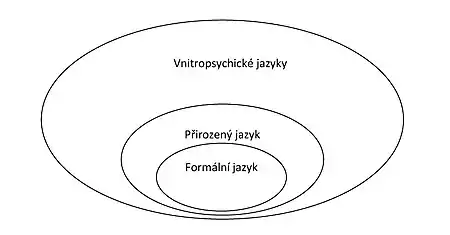
V roce 1956 Noam Chomsky vytvořil hierarchii čtyř tříd formálních gramatik generujících umělé formální jazyky. Chomského hierarchie dělí formální gramatiky do tříd s rostoucí vyjadřovací silou (schopností jazyka popisovat, reprezentovat jistou množinu znalostí) – každá následná třída je schopna generovat širší skupinu formálních jazyků než předchozí třída, ne všechny třídy jsou disjunktní. Každému typu oněch gramatik odpovídá stroj – automat, od gramatiky typu 3 (regulární gramatiky) generující regulární jazyky, jíž odpovídá konečný automat, po gramatiky typu 0 (frázové gramatiky) generující rekurzivní jazyky, jímž odpovídá Turingův stroj – univerzální číslicový počítač. Všechny formální jazyky jsou vázány striktním zákazem vnitřní vágnosti, tedy vnitřní vágnost jakékoli jejich interpretace musí být nulová a tyto jazyky mohou používat pouze vágnost vnější. Na uvedenou Chomského hierarchii můžeme navázat ve smyslu jazyků s postupně se zvyšující vyjadřovací silou, avšak nyní neformálními jazyky, u nichž zákaz vnitřní vágnosti neplatí. Vnitropsychické jazyky (velká vágnost znalostí – nejvyšší vyjadřovací síla) jsou schopny reprezentovat větší množinu znalostí než přirozený jazyk (menší vágnost znalostí než vnitropsychické jazyky) – některé znalosti člověkem běžně a úspěšně používané, jsou nesdělitelné. Důvod i s příkladem je podrobně uveden v[3]. Jen část poznaného je člověk schopen transformovat do přirozeného jazyka (sdělovat). Přirozený jazyk je schopen reprezentovat větší množinu znalostí než umělý formální jazyk (nulová vnitřní vágnost)[8]. Toto porovnání jazyků vypovídá o rozdílných schopnostech člověka a stroje (automatu, počítače popsaného příslušnou Chomského gramatikou), co do možné šíře záběru poznání a zpracování poznané informace. Diskrétní filtr poznání velice omezuje oblast poznání. Filtr vágnosti umožňuje vágně znát mnohé, diskrétní filtr umožňuje exaktně znát nemnohé. V následujícím obrázku je zobrazena hierarchie jazyků se zvyšující se vyjadřovací silou v závislosti na zvyšující se vágnosti. V množině označené Formální jazyk, se nalézá Chomského hierarchie jazyků.

Hierarchie jazyků

Lze se setkat s názory některých badatelů, že reálný svět je vágní. V tomto směru je třeba si všimnout jak poznání, tak jazyka, který je poznané schopen zaznamenat – reprezentovat. Mnozí z nich zapomínají na to, že mezi věděním člověka o reálném světě a reálným světem samým, je jediný most a tím je akt poznání, o nepoznaném nic nevíme. Vlastnosti reálného světa, je člověk schopen hodnotit pouze prostřednictvím poznání. Typy poznání jsou dva: poznání přirozené a umělé Newtonovo. Jazyk navazující na poznání musí odpovídat typu poznání, vyjadřovací sílou a mírou neurčitosti.

K poznání.

Víra, že zápas s neurčitostí lze vyhrávat stálým zlepšováním zobrazovacích nástrojů a metod poznání reality, zlepšováním přesnosti měření a technologie výroby, byla vyvrácena formulací Heisenbergova principu neurčitosti (1927). Heisenbergův princip charakterizuje poznání, neříká, že neurčitá je realita, říká jaký model reality je člověk schopen získat. Příroda v něm lidskému poznání říká: dost, dál tě člověče, nepustím. Heisenbergův princip neurčitosti říká, že existují vzájemně svázané dvojice veličin (říká se jim konjugované), pro které platí, že čím přesněji poznáme hodnotu jedné veličiny, tím méně přesně můžeme změřit hodnotu druhé veličiny. Např. pro dvojici hybnosti p a polohy x (délková souřadnice) libovolného volného reálného objektu platí vztah neurčitosti:

                 ∆x * ∆p  ≥ h/4π 

kde: h je Planckova konstanta, h = 6,6262•10–34 J•s,

∆ značí interval příslušné veličiny, v němž se její hodnota může pohybovat.

Vztah říká, že součin z intervalů neurčitosti hodnot polohy x a hybnosti p, je větší, nanejvýš roven hodnotě Planckovy konstanty lomené 4π. Jinými slovy: Vztah neurčitosti říká, že nelze současně přesně poznat (změřit) polohu a hybnost reálného objektu. Čím přesněji určíme hybnost, tím méně přesně určíme polohu částice a naopak. Heisenbergův princip tak ukazuje, že kognitivní model reality bude vždy obsahovat neurčitost. Je to neurčitost poznání.

Princip neurčitosti platí v celém hmotném světě, uplatňuje se však tím významněji, čím menší hmotnost má dotyčný objekt. Fatální bariérou pro poznání se tento princip stává až pro objekty mikrosvěta (světa částic) s velmi malou hmotností, neboť Planckova konstanta je velmi malé číslo. Heisenbergův princip neurčitosti platí pro celý hmotný svět a je principem neurčitosti poznání. V makrosvětě se uplatňuje nepatrně a v mikrosvětě velevýznamně. Poznání s nulovou neurčitostí tedy neexistuje v samém principu.

Vágnost či jiná forma neurčitosti může být vlastností poznání, nelze ji přisuzovat reálnému světu, je to vlastnost mostu, který člověka s tímto světem informačně spojuje.

Ke sdělování:

Doslovnost a obraznost v komunikaci[9] jsou dva pojmy označující dva způsoby lidské komunikace. Prvý klade důraz na úlohu jazyka a jeho přesnosti, druhý na porozumění lidským vhledem a citem mezi komunikujícími, na metaforu, symboličnost. Obvykle se spojují s úlohou každé z hemisfér lidského mozku podle amerického neurologa Rogera Wolcotta Sperryho (1913 – 1994) a převahou aktivity jedné z hemisfér u toho kterého člověka. Levá hemisféra dává lidské osobnosti racionalitu, logiku, objektivistický způsob myšlení a nahlížení na svět, schopnost vědecké práce. Pravá hemisféra mu dává citovou bohatost, obrazotvornost, schopnost umělecké tvorby. U každého lidského jedince se obě hemisféry podílejí v jistých, jemu vlastních proporcích na jeho nazírání na svět, uvažování a schopnosti a způsobu sdělování. O doslovnost (konotace blížící se exaktní interpretaci) se snaží věda, a absolutní doslovnosti (nulový sémantický diferenciál, tedy exaktní interpretace) dosáhla exaktní věda. Cesta k doslovnosti vede k budování terminologických soustav. Základní pojmy jsou postaveny na konsensu, odvozené na definicích s použitím základních pojmů. V běžné lidské komunikaci se neklade velký důraz na doslovnost, jsme zvyklí na vhled a vstřícnost, symboliku slov, tedy spíš na složku obraznosti, ta více vyhovuje neodmyslitelné lidské emocionalitě.

Porozumění úloze vágnosti umožňuje pochopit principy přirozeného a umělého poznání, porozumět podstatě exaktních věd, a pochopit propastný rozdíl mezi lidským a počítačovým zpracování informace, a tak i rozeznat některé scestné postupy a úvahy v oboru Umělé inteligence[8].