Théveninova věta

Odpojení ideálních zdrojů napětí a proudu

1. Označíme si 2 svorky
2. Obvod si rozdělíme na dvě části - zátěž (prvek, větev na které chceme vypočítat tekoucí proud) a druhá část bude zbytek lineární soustavy
3. Podle Theveninovy věty lze zbytek lineární soustavy nahradit skutečným zdrojem napětí. Ten je tvořen vnitřním napětím (ten určíme jako napětí naprázdno mezi svorkami) a vnitřním odporem (ten určíme jako celkový odpor lineární soustavy mezi svorkami při odpojené zátěži, když zdroje vyřadíme)
4. Při výpočtu nahradíme zdroje jejich vnitřními odpory, tj. ideální zdroj napětí (IZN) zkratujeme a ideální zdroj proudu (IZP) rozpojíme.

Lineární obvod u kterého chceme zjistit proud na rezistoru ${\displaystyle R_{2}}$

Mějme obvod u kterého chceme vypočítat proud na rezistoru ${\displaystyle R_{2}}$. Viz obrázek.

Nejdříve si označíme svorky (např. ${\displaystyle X}$ a ${\displaystyle Y}$) na rezistoru R2 a tento rezistor odpojíme. Tento rezistor tvoří tzv. zátěž. (Obr. 1)

Obr. 1

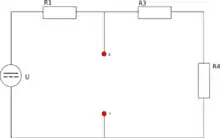
V tomto obvodu bez připojeného rezistoru R2 vypočítáme proud, který protéká obvodem. Ten se rovná podle Ohmova zákona:

${\displaystyle I_{0}={\frac {U}{R1+R3+R4}}}$

Vnitřní napětí náhradního zdroje určíme jako napětí mezi svorkami ${\displaystyle X}$ a ${\displaystyle Y}$. Proud ${\displaystyle I_{0}}$ vytváří na jednotlivých rezistorech úbytky napětí ${\displaystyle U_{1}}$, ${\displaystyle U_{3}}$, ${\displaystyle U_{4}}$. Ty se rovnají:

${\displaystyle U_{1}=R_{1}I_{0}}$

${\displaystyle U_{3}=R_{3}I_{0}}$

${\displaystyle U_{4}=R_{4}I_{0}}$

Obvod si můžeme pro lepší pochopení překreslit (Obr. 2)

Obr. 2

a zapojení vlastně vytváří nezatížený dělič napětí. V tomto případě se napětí mezi svorkami ${\displaystyle XY}$ rovná:

${\displaystyle U_{XY}=U-U_{1}=U_{3}+U_{4}}$

Při výpočtu vnitřního odporu náhradního zdroje nejprve odpojíme zdroj napětí, a to tak, že tento zdroj zkratujeme. Překreslený obvod je na obrázku č. 3.

Obr. 3

Tento obvod zjednodušíme a výsledný odpor se rovná vnitřnímu odporu zdroje (${\displaystyle R=R_{i}}$):

${\displaystyle R_{i}={\frac {R_{1}(R_{3}+R_{4})}{R_{1}+R_{3}+R_{4}}}}$

Výsledné schéma náhradního obvodu se skutečným zdrojem napětí je vidět na obrázku č. 4.

Obr. 4

Teď, když známe svorkové napětí a vnitřní odpor zdroje, můžeme vypočítat proud tekoucí rezistorem ${\displaystyle R_{2}}$:

${\displaystyle I_{2}={\frac {U_{xy}}{R_{i}+R_{2}}}}$

• Nortonův teorém
• Kirchhoffovy zákony
• Vnitřní odpor