Semikubická parabola
Semikubická parabola (též Neilova parabola) je rovinná kubika, tj. algebraická rovinná křivka 3. stupně, kterou lze v kartézské soustavě souřadnic vyjádřit rovnicí
- ,
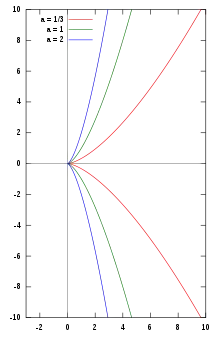
Semikubické paraboly pro různé hodnoty a
kde je konstanta a .
Další vyjádření
Vlastnosti
Speciálními případy této křivky jsou evoluta paraboly:
a katakaustika Tschirnhausenovy kubiky:
Sama je speciálním případem eliptické křivky v Legendrově normální formě:
Křivka se někdy označuje po anglickém matematikovi W. Neilovi (1637–1670), který ji v roce 1657 objevil.
Byla první netriviální algebraickou křivkou, u které byla vypočítána délka oblouku (mezi hrotem a bodem s argumentem t při výše uvedené parametrizaci):
Související články
Externí odkazy
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.