Prohození hodnot XORem
Prohození hodnot XORem je v programování jedním z algoritmů, kterými lze dosáhnout prohození hodnot dvou proměnných bez použití pomocné dočasné proměnné. Používá k tomu bitovou operaci úplné disjunkce.
Algoritmus
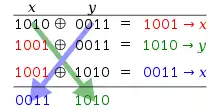
Algoritmus se skládá ze tří kroků, přičemž všechny využívají operaci XOR:
X := X xor Y
Y := Y xor X
X := X xor Y
Jednotlivé řádky obvykle přímo odpovídají instrukcím jazyka symbolických adres respektive přímo strojovým instrukcím. Následující příklad uvádí instrukce na platformách IBM System/370 a x86:
| Pseudokód | IBM System/370 | x86 |
|---|---|---|
X := X XOR Y | XR R1,R2 | xor eax, ebx |
Y := Y XOR X | XR R2,R1 | xor ebx, eax |
X := X XOR Y | XR R1,R2 | xor eax, ebx |
Pro funkčnost algoritmu je zásadní, aby jeho vstupem nebylo dvakrát stejné umístění. Protože totiž pro každé x je výsledek operace x XOR x nulový, bylo by hned v prvním kroku toto umístění vynulováno a tím jeho hodnota ztracena.
Důkaz správnosti
Správnost algoritmu je odvozena z toho, že binární operace XOR (značená ) na bitových řetězcích pevné délky splňuje následující čtyři vlastnosti:
- L1. Komutativitu:
- L2. Asociativitu:
- L3. Existenci neutrálního prvku: existuje prvek, značený 0, pro který platí pro každé
- L4. Každý prvek je sám sobě inverzním: pro každé , .
| Krok | Operace | Registr 1 | Registr 2 | Redukce dle vlastnosti |
|---|---|---|---|---|
| 0 | Úvodní hodnota | — | ||
| 1 | R1 := R1 XOR R2 | — | ||
| 2 | R2 := R1 XOR R2 | L2 L4 L3 | ||
| 3 | R1 := R1 XOR R2 | L1 L2 L4 L1 L3 |
Varianty
Podobný algoritmus lze realizovat pomocí sčítání a odčítání:
void addSwap (unsigned int *x, unsigned int *y)
{
if (x != y) {
*x = *x + *y;
*y = *x - *y;
*x = *x - *y;
}
}
Jeho správnost je ale závislá na tom, že nedojde k celočíselnému přetečení. Je-li například práce na celých číslech realizována s podporou libovolné přesnosti nebo v rámci modulární aritmetiky, algoritmus funguje. Například v rámci jazyka C tento algoritmus funguje, neboť sčítání a odčítání dle standardu odpovídá operacím v cyklické grupě , kde je počet bitů.
Vzhledem k dodatečnému požadavku na vlastnosti sčítání je tato varianta používána ještě méně než varianta základní.
Výhody a nevýhody
Nevýhody:
- Je-li v daném kontextu dost volných registrů procesoru, pak bude prohození hodnot pomocí nějakého volného pravděpodobně rychlejší
- Moderní počítačové architektury často využívají překrývané zpracování strojových instrukcí. To umí rychle zpracovávat kód, ve kterém zpracování instrukce nezávisí na výsledku instrukcí těsně předcházejících. V tomto algoritmu na sebe všechny tři instrukce bezprostředně navazují, takže překrývané zpracování nemůže být využito a procesor je bude zpracovávat pomalu postupně.
- Pro programátora, který postup nezná, se jedná o obtížně pochopitelný trik, jehož prokouknutí ho při studování kódu zbytečně zdrží.
Výhody:
- Instrukce XOR má na některých architekturách úsporné kódování (tedy využití algoritmu může šetřit instrukční cache)
- V rámci části kódu náročné na volné registry může mít ušetření pomocného registru zásadní dopady na výkon.
- Na jednočipových počítačích a jiných malých platformách může mít smysl i ušetření pomocné operační paměti
Reference
V tomto článku byl použit překlad textu z článku XOR swap algorithm na anglické Wikipedii.