Phillipsova křivka
Phillipsova křivka je ekonomický model s jednou rovnicí, pojmenovaný podle Williama Phillipse, který popisuje inverzní vztah mezi mírami nezaměstnanosti a odpovídajícími mírami růstu mezd, které jsou výsledkem ekonomiky. Jednoduše řečeno, snížená nezaměstnanost (tj. Zvýšená úroveň zaměstnanosti) v ekonomice bude korelovat s vyšší mírou růstu mezd. [1].
Samotný Phillips neuvedl, že existuje nějaký vztah mezi zaměstnáním a inflací; tato představa byla triviální dedukcí z jeho statistických zjištění
Historie
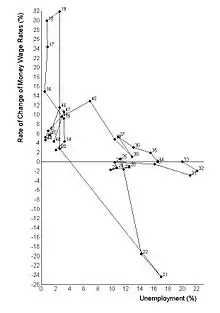
William Phillips, ekonom narozený na Novém Zélandu, napsal v roce 1958 článek s názvem The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom (Vztah mezi nezaměstnaností a mírou změn sazeb míry peněz ve Spojeném království), který byl publikován v čtvrtletním časopise Economica.[1] V článku Phillips popisuje, jak pozoroval inverzní vztah mezi změnami mzdy a nezaměstnaností, v Britské ekonomii ve zkoumaném období. Podobné modely byly nalezeny i v jiných zemích a v roce 1960 Paul Samuelson a Robert Solow vzali Phillipsovu práci a jasně ukázali vztah mezi inflací a nezaměstnaností: Když inflace byla vysoká, nezaměstnanost byla nízká a naopak. [2]
Ve dvacátých letech minulého století americký ekonom Irving Fisher tento vztah Phillipsovy křivky zaznamenal. Nicméně, Phillipsova původní křivka popisovala chování peněžních mezd. [3]
V následujících letech, po tomto článku z roku 1958, mnozí ekonomové ve vyspělých průmyslových zemích věřili, že jeho výsledky ukazují, že mezi inflací a nezaměstnaností je trvale stabilní vztah. Jedním z důsledků bylo pro vládní politiku to, že vlády mohly ovládat nezaměstnanost a inflaci pomocí keynesiánské politiky. Vlády by tedy mohly tolerovat poměrně vysokou míru inflace, neboť by to vedlo k nižší nezaměstnanosti – došlo by k odrazu mezi inflací a nezaměstnaností. Například měnová politika nebo fiskální politika by mohla být použita ke stimulaci hospodářství, zvýšení hrubého domácího produktu a snížení míry nezaměstnanosti. Při pohybu podél Phillipsovy křivky by to vedlo k vyšší míře inflace a k nárůstu nákladů na nižší míru nezaměstnanosti. Ekonom James Forder tvrdí, že tento názor je historicky nepravdivý, že ani ekonomové, ani vlády tuto představu nezohlednili a "Phillipsův křivkový mýtus" byl vynález sedmdesátých let. [4]
Od roku 1974 bylo uděleno sedm Nobelových cen ekonomům za, kromě jiného, kritiku některých variant Phillipsovy křivky. Jedna z těchto kritik je založena na zkušenostech Spojených států v 70. letech, které měly zároveň vysokou míru nezaměstnanosti a vysokou inflaci. Mezi autory, kteří získali tyto ceny, patří Thomas Sargent, Christopher Sims, Edmund Phelps, Edward Prescott, Robert A. Mundell, Robert E. Lucas, Milton Friedman, a F.A. Hayek.[5]
Stagflace
V sedmdesátých letech zaznamenala řada zemí vysokou míru inflace i nezaměstnanosti, známou také jako stagflace. Teorie založená na Phillipsově křivce naznačuje, že se to nemůže stát, a křivka se dostala pod útok skupiny ekonomů s vedením Miltona Friedmana. Friedman tvrdil, že vztah Phillipsovy křivky je jen krátkodobý fenomén. V tomto následoval Samuelsona a Solowa (1960), který napsal: "Všechny naše diskuse byly formulovány v krátkodobých termínech, které se zabývají tím, co by se mohlo stát v příštích několika letech.”[2]
Současnost
Většina ekonomů už nepoužívá Phillipsovu křivku v původní podobě, protože se ukázalo že příliš zjednodušuje skutečnost [6]. To lze pozorovat ve zběžné analýze údajů o inflaci a nezaměstnanosti v USA z let 1953-92. Neexistuje žádná samostatná křivka, která by vyhovovala datům, ale existují tři hrubé agregace – 1955-71, 1974-84 a 1985-92 – z nichž každá ukazuje celkový “svah” směrem dolů, ale na třech velmi rozdílných úrovních s náhle se vyskytujícími posuny.[7]
Modifikované formy Phillipsovy křivky, které berou v úvahu inflační očekávání,dodnes zůstávají vlivné. Tato teorie se skládá z několika jmen s různými detaily, ale všechny moderní verze rozlišují mezi krátkodobými a dlouhodobými účinky na nezaměstnanost. Moderní modely Phillipsových křivek zahrnují krátkodobou Phillipsovu křivku a dlouhodobou Phillipsovu křivku. Je to proto, že v krátkodobém horizontu je obecně mezi inflací a mírou nezaměstnanosti poměrně inverzní vztah; jak je znázorněno na klesající krátkodobé Phillipsově křivce. Z dlouhodobého hlediska se tento vztah rozpadá a ekonomika se nakonec vrací do přirozené míry nezaměstnanosti, bez ohledu na míru inflace.[8]
Edmund Phelps a Milton Friedman argumentovali, že "krátkodobá Phillipsova křivka" se také nazývá "Phillipsova křivka, zvyšující se dle inflačního očekávání”(neboť její posun nastává tehdy, když inflační očekávání vzroste). Z dlouhodobého hlediska to znamená, že měnová politika nemůže ovlivnit nezaměstnanost, která se přizpůsobuje její "přirozené míře" nazvané také "NAIRU" nebo "dlouhodobá Phillipsova křivka". Tato dlouhodobá "neutralita" měnové politiky však umožňuje krátkodobé fluktuace a schopnost měnového orgánu dočasně snížit nezaměstnanost zvýšením stálé inflace a naopak.[9]
Rovnice, jako je Phillipsova křivka rozšířená o očekávání, se také objevuje v mnoha nedávných nových keynesiánských dynamických stochastických modelech obecné rovnováhy. V těchto makroekonomických modelech s nepříznivými cenami, existuje pozitivní vztah mezi mírou inflace a úrovní poptávky, a tudíž i negativním vztahem mezi mírou inflace a mírou nezaměstnanosti. Tento vztah se často nazývá "novou keynesiánskou Phillipsovou křivkou". Podobně jako Phillipsova křivka rozšířená o očekávání, naznačuje nová keynesiánská Phillipsova křivka, že zvýšená inflace může dočasně snížit nezaměstnanost, ale nemůže ji snížit trvale. Dva vlivné dokumenty, které obsahují novou keynesiánskou Phillipsovu křivku, jsou Clarida, Galí, a Gertler (1999),[10] a Blanchard a Galí (2007).[11]
Matematika
Existují nejméně dvě různá matematická odvození Phillipsovy křivky. Jako první, existuje tradiční – keynesiánská verze. A jako druhá je nová klasická verze spojená s Robertem E. Lucasem, Jr.
Tradiční Phillipsova křivka
Původní literatura nebyla založena na samostatné aplikaci ekonomické teorie. Namísto toho byla založena na empirických zobecňováních. Až poté se ekonomové snažili rozvíjet teorie, které odpovídají datům.
Určení peněžní mzdy
Tradiční příběh Phillipsovy křivky začíná mzdovou Phillipsovou křivkou, jakou popsal sám Phillips. To popisuje míru růstu peněžních mezd (gW). Zde (i níže) je operátor g ekvivalentem "procentuálního růstu" proměnné, která následuje:
"Mzdová míra peněz" (W) je zkratka pro celkové mzdové náklady na pracovníka produkce, včetně dávek a daní ze mzdy. Důraz je kladen pouze na peněžní mzdy výrobních pracovníků, protože (jak je uvedeno níže) jsou tyto náklady rozhodující pro rozhodování firem o cenách.
Tato rovnice nám říká, že růst peněžních mezd vzrůstá s vývojovou mírou růstu peněžních mezd (naznačených horním indexem "T") a klesá s mírou nezaměstnanosti (U). Předpokládá se, že funkce f () se monotónně zvyšuje s U tak, že tlumení nárůstu peněžní mzdy nezaměstnaností je znázorněno negativním znaménkem ve výše uvedené rovnici.
S touto rovnicí existuje mnoho různých přístupů. Hlavní přístup znázorňuje měnové mzdy, které jsou stanoveny bilaterálními jednáními (dohodami) v rámci částečného bilaterálního monopolu: jak stoupá míra nezaměstnanosti, všechna ostatní pracovní síla upadá, právě proto, aby pracovníci byli neschopní zvýšit svou mzdu tváří v tvář odporu zaměstnavatele.
Během sedmdesátých let tento přístup musel být změněn, protože (jak Abba Lerner navrhl ve čtyřicátých letech minulého století) se pracovníci snaží udržet krok s inflací. Od sedmdesátých let minulého století byla rovnice změněna tak, aby představila roli inflačních očekávání (nebo očekávané inflace, gPex). Toto vytváří očekávanou mzdovou křivku Phillipsovy křivky:
Zavedení inflačních očekávání do rovnice znamená, že skutečná inflace může mít zpětnou vazbu k inflačnímu očekávání a způsobit další inflaci. Ekonom James Tobin označil poslední období jako "inflační nečinnost", protože v současném období existuje inflace, která představuje inflační "impuls", který zbyl z minulosti.
Zahrnovalo to mnohem více než pouhá očekávání, včetně mzdově cenové spirály. V této spirále se zaměstnavatelé snaží chránit zisky, zvyšováním svých cen, a zaměstnanci se snaží udržet krok s inflací, aby ochránili své skutečné mzdy. Tento proces se může stát sebenaplňujícím se proroctvím.
Parametr λ (který je považován za konstantní v jakémkoli časovém období) představuje míru, do níž mohou zaměstnanci získat nárůst peněžních mezd, aby udrželi krok s očekávanou inflací a zabránili tak poklesu očekávaných reálných mezd. Obvykle se předpokládá, že se tento parametr dlouhodobě rovná jedné.
Kromě toho byla funkce f () upravena tak, aby představila myšlenku nezrychlující se míry inflace nezaměstnanosti (NAIRU) nebo co se někdy nazývá "přirozená" míra nezaměstnanosti nebo inflační prahová míra nezaměstnanosti:
- [1] gW = gWT - f(U − U*) + λ·gPex.
Zde je U NAIRU. Jak je uvedeno níže, pokud U <U , inflace má tendenci zrychlovat. Podobně, pokud U> U , inflace má tendenci zpomalovat. Předpokládá se, že f (0) = 0, takže když U = U (termín f vypadne z rovnice.)
Může se zdát, že v rovnici [1] jsou gWT a gPex nadbytečné, a že hrají podobnou roli. Nicméně za předpokladu, že λ je rovný jedné, je vidět, že tomu tak není. Pokud je trendová tendence růstu peněžních mezd rovna nule, pak případ, kdy U = U, znamená, že gW se rovná očekávané inflaci. To znamená, že očekávané reálné mzdy jsou konstantní.
V jakékoli přiměřené ekonomice by ovšem konstantní očekávané reálné mzdy mohlo být v souladu pouze se skutečnými reálnými mzdami, které jsou konstantní v dlouhodobém období. To neodpovídá ekonomickým zkušenostem v USA nebo v žádné jiné významné průmyslové zemi. I když reálné mzdy v posledních letech výrazně nevzrostly, došlo během desetiletí k významnému nárůstu.
Alternativou je předpokládat, že tempo růstu peněžních mezd se rovná tempu růstu průměrné produktivity práce (Z). To znamená:
- [2] gWT = gZT.
Podle předpokladu [2], kdy U se rovná U a λ rovná jedné, se očekává, že reálná mzda vzroste s produktivitou práce. To by bylo v souladu s ekonomikou, ve které se zvyšují reálné mzdy s produktivitou práce. Odchylky reálných mzdových trendů od vývoje produktivity práce lze vysvětlit odkazem na jiné proměnné v modelu.
Rozhodování o cenách
Další podstatný faktor je cenové chování. Standardním předpokladem je, že trhy jsou nedokonale konkurenceschopné, kde většina podniků má určitou moc stanovovat ceny. Takže model předpokládá, že průměrná obchodní aktivita stanoví jednotnou cenu (P) jako tkz. "markup" (M) na jednotkové náklady práce ve výrobě, měřené při standardní míře využití kapacity (např. U 90% využití zařízení a zařízení) a poté se přidají náklady na jednotku materiálu.
Standardizace zahrnuje i pozdější ignorování odchylek od trendů produktivity práce. Předpokládejme například, že růst produktivity práce je stejný jako růst produktivity práce a současná produktivita se rovná její hodnotě trendu:gZ = gZT and Z = ZT.
Označení odráží jak stupeň tržní síly firmy, tak rozsah, v němž je třeba platit režijní náklady. Jiným způsobem, stejně jako M, stoupá s mocí firmy stanovit ceny nebo s nárůstem režijních nákladů vzhledem k celkovým nákladům.
Takže cena vychází z této rovnice:
P = M × (jednotkové náklady práce) + (náklady na jednotkové materiály)= M × (celkové náklady na výrobu v produkci) / (množství výstupu) + UMC
UMC představuje jednotkové náklady na suroviny (celkové náklady na suroviny dělené celkovým výstupem). Takže rovnici lze přepracovat jako:
P = M × (výrobní náklady na zaměstnance) / (výstup na pracovníka produkce) + UMC.
Tato rovnice může být dána takto:
P = M × (průměrná peněžní mzda) / (produkční produktivita práce) + UMC = M × (W / Z) + UMC
Předpokládejme, že průměrná cena (M) a UMC jsou konstantní. Na druhé straně produktivita práce roste, stejně jako předtím. Proto rovnice určující míru inflace (gP) je: gP = gW – gZT.
Cena
V kombinaci s křivkou Phillipsovy mzdy [rovnice 1] a předpokladem uvedeným výše o trendovém chování peněžních mezd [rovnice 2], tato rovnice cenových inflace nám dává jednoduchou cenu za očekávání Phillipsova křivka:
gP = −f(U − U*) + λ·gPex.
Někteří se domnívají, že můžeme jednoduše přidat do gUMC, tempo růstu UMC, abychom představili úlohu šoků v nabídce (takových, které sužovaly USA v 70. letech). To vytváří standardní krátkodobou Phillipsovu křivku:
gP = −f(U − U*) + λ·gPex + gUMC.
Ekonom Robert J. Gordon toto nazval "Trojúhelníkový model", protože vysvětluje krátkodobé inflační chování třemi faktory: poptávkovou inflací (kvůli nízké nezaměstnanosti), nabídkovou inflací (gUMC) a inflačními očekáváními nebo inerciální inflací.
V dlouhodobém horizontu se předpokládá, že inflační očekávání dosahují a rovnají se skutečné inflaci, takže gP = gPex. To představuje dlouhodobou rovnováhu úprav očekávání. Část této úpravy může zahrnovat přizpůsobení očekávání zkušenosti se skutečnou inflací. Jiný může zahrnovat odhady lidí v ekonomice na základě jiných důkazů. (Poslední myšlenka nám dala představu o takzvaných racionálních očekáváních.)
Očekávaná rovnováha nám dává dlouhodobou Phillipsovu křivku. Zaprvé, s λ méně než jedna:
gP = [1/(1 − λ)]·(−f(U − U*) + gUMC).
To není nic jiného než strmější verze krátkodobé Phillipsovy křivky (výše). Inflace vzrůstá s poklesem nezaměstnanosti, zatímco toto spojení je silnější. To znamená, že nízká míra nezaměstnanosti (nižší než U ) bude spojena s vyšší mírou inflace v dlouhodobém horizontu, než v krátkodobém horizontu. K tomu dochází, protože skutečná situace s vyšší mírou inflace, která se projevila v krátkodobém horizontu, je zdrojem inflačních očekávání, což dále zvyšuje míru inflace. Stejně tak při vysoké míře nezaměstnanosti (vyšší než U ) vedou k nízké míře inflace. Ty zase povzbuzují nižší inflační očekávání, takže inflace sama opět klesá.
Krátkodobá platnost
Jak ukázal Milton Friedman, tato substituce (často označovaná jako „trade-off“, v doslovném překladu „kompromis“[12]) platí pouze v krátkém období, kdy se nemění očekávaná míra inflace. Dochází-li ke snižování nezaměstnanosti, roste tlak zaměstnanců na zvyšování mezd a zároveň se v delším období zvyšuje procento očekávané inflace. V tento moment dochází k posunu krátkodobé Phillipsovy křivky na vyšší úroveň, což znamená vyšší míru inflace při stejné míře nezaměstnanosti. Dlouhodobá Phillipsova křivka se ustálí v místě přirozené míry nezaměstnanosti – vertikálně v grafu, kde je na ose X vynesena míra nezaměstnanosti a na Y míra inflace. Jakékoliv snahy dosáhnout nižší nezaměstnanosti, než jaká je její přirozená míra, zvyšují inflační očekávání a vedou v krátkodobém měřítku k růstu zaměstnanosti, v dlouhodobém ovšem pouze k růstu inflace, neboť nezaměstnanost se vrátí na svoji přirozenou míru.
„Dlouhodobě je míra nezaměstnanosti na tzv. přirozené míře a je slučitelná s libovolnou mírou inflace. Původní Phillipsova inverzní závislost stále platí, ale jen v krátkém období. Jde tedy o případ dlouhodobé Phillipsovy křivky, která je kolmá. Přirozená míra nezaměstnanosti je taková míra nezaměstnanosti, při které jsou pracovní trhy v rovnováze - neprojevuje se ani nedostatek pracovníků, ani nedobrovolná nezaměstnanost.“[13]
NAIRU
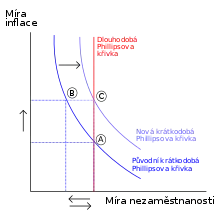
V 70. letech 20. století vznikly nové teorie, jako teorie racionálního očekávání a NAIRU což je zkratka pro.: non-accelerating inflation rate of unemployment (nezrychlující míra inflace nezaměstnanosti), která vysvětlila, jak může stagflace nastávat. Později teorie NAIRU, známá též jako "přirozená míra nezaměstnanosti", (typ přirozené míry nezaměstnanosti při níž nedochází k akceleraci, ani k deceleraci, míry růstu inflace) rozlišuje mezi "krátkodobou" Phillipsovou křivkou a "dlouhodobou" křivkou. Krátkodobá Phillipsova křivka zprvu vypadala jako klasická Phillipsova křivka, ale v dlouhodobém měřítku se změnila, podle toho, jak se měnilo racionální očekávání. Z dlouhodobého hlediska byla přirozená míra nezaměstnanosti v souladu se stabilní mírou inflace. Dlouhodobá Phillipsova křivka byla tedy vertikální, takže mezi inflací a nezaměstnaností nedošlo k žádnému kompromisu. Edmund Phelps získal Nobelovu cenu za ekonomii v roce 2006, částečně za tuto práci. Nicméně teorie, racionálního očekávání a NAIRU, byla ve skutečnosti velmi dobře pochopena (i když ne formálně) předtím, než Phelps začal na teorii očekávání vůbec pracovat.[14]
V diagramu je dlouhodobá Phillipsova křivka svislá červená čára. Teorie NAIRU říká, že pokud míra nezaměstnanosti dosáhne míry definované tímto řádkem, inflace bude stabilní. Nicméně v situaci krátkodobé Phillipsovi křivky, političtí činitelé budou muset čelit kompromisu, mezi inflací a mírou nezaměstnanosti, který je v grafu označen jako "počáteční krátkodobá Phillipsova křivka". V tento okamžik mohou dočasně snížit míru nezaměstnanosti, a přesunout se z bodu A do bodu B (můžeme vidět v grafu) prostřednictvím expanzivní politiky. Podle NAIRU však využití tohoto krátkodobého řešení, s pomocí expanzní politiky, zvýší inflační očekávání. Pokud tedy posuneme krátkodobou křivku směrem doprava na "novou krátkodobou Phillipsovu křivku", přesuneme tím i bod rovnováhy z B na C (toto opět můžeme vidět v grafu). Tím se sníží nezaměstnanost pod "přirozenou míru", bude dočasná a povede pouze k vyšší inflaci v dlouhodobém horizontu.
Vzhledem k tomu, že krátkodobá křivka se v důsledku pokusu o snížení nezaměstnanosti posunuje směrem ven, expanzní politika zhoršuje využitelný potenciál mezi nezaměstnaností a inflací. To znamená, že má za následek vyšší inflaci, při každé krátkodobé míře nezaměstnanosti. Název "NAIRU" vzniká, neboť skutečná nezaměstnanost, znázorněna pod křivkou, snižuje inflaci, zatímco nezaměstnanost, znázorněna nad křivkou, inflaci zpomaluje. Se skutečnou mírou nezaměstnanosti (která se rovná křivce), je inflace stabilní, není ani zrychlená, ani zpomalená. V minulosti jedním praktickým využitím tohoto modelu bylo poskytnutí vysvětlení stagflace, která překonala tradiční Phillipsovu křivku.
Teorie racionálních očekávání uvedla, že očekávání inflace se rovnalo tomu, co se skutečně stalo, až na některé drobné a dočasnými chyby. To zase naznačovalo, že krátkodobé období bylo tak krátké, že neexistovalo: jakákoli snaha o snížení nezaměstnanosti pod úrovní NAIRU by například okamžitě způsobila růst inflačních očekávání, což znamená, že politika by selhala. Nezaměstnanost se nikdy neodchýlí od NAIRU, s výjimkou náhodných a přechodných chyb při vytváření očekávání ohledně budoucí míry inflace. Z tohoto hlediska byla jakákoli odchylka skutečné míry nezaměstnanosti od NAIRU iluzí.
Avšak v devadesátých letech v USA bylo stále více jasné, že NAIRU neměla jedinečnou rovnováhu a mohla se změnit nepředvídatelným způsobem. Koncem devadesátých let se skutečná míra nezaměstnanosti snížila pod 4 % pracovní síly, což je mnohem nižší než téměř všechny odhady NAIRU. Přesto, ale Inflace zůstala spíše mírná, než aby se zrychlila, a Phillipsova křivka se stala předmětem debaty, společně i s NAIRU. Navíc i pojem racionální očekávání se stal předmětem mnoha pochybností, když se ukázalo, že hlavní předpoklad modelů, které z něho vycházejí, spočívá v tom, že v ekonomice existuje „jedinečná“ rovnováha, která je předem stanovena nezávisle na podmínkách poptávky. Zkušenosti z devadesátých let proto naznačují, že tento předpoklad je ve skutečnosti nemožné aplikovat.
Teoretické otázky
Z počátku Phillipsova křivka byla jen objekt empirického pozorování s cílem najít teoretické vysvětlení pro tento jev. Konkrétně se pokusili přijít na to, zda je vztah inflace a nezaměstnanosti kauzální nebo korelační. Existuje několik hlavních vysvětlení pro krátkodobou pravidelnost Phillipsovy křivky.
Pro Miltona Friedmana existuje krátkodobá korelace mezi inflačními “šoky” a zaměstnaností. Když dojde k inflačnímu “šoku”, neboli nečekané vlně inflace, pracovníci jsou v podstatě napáleni, přijmou tedy nižší plat, protože nevidí okamžitý pokles reálných mezd. Firmy je najímají, protože vidí inflaci naopak jako, možnost pro získání vyššího finančního obratu daných nominálních mezd. Jedná se o pohyb podél Phillipsovy křivky se změnou A. Nakonec pracovníci zjistí, že skutečná mzda klesla, a tak dožadují vyššího platu. To způsobuje, že se Phillipsova křivka posunuje směrem vzhůru a doprava, stejně jako u B. Některé výzkumy zdůrazňují, že některé implicitní a vážné předpoklady jsou ve skutečnosti v pozadí Friedmanovy Phillipsovy křivky. Tato informační asymetrie a zvláštní model pružnosti cen a mezd, oba jsou nezbytné, pokud chceme zachovat mechanismus, který Friedman prezentuje. Nicméně, jak tvrdí různé diskuse namítají, tyto předpoklady zůstávají Friedmanem zcela nevýrazné a teoreticky nezohledněné.[15]
Ekonomové, jako je například Edmund Phelps, tuto teorii odmítají, protože naznačuje, že pracovníci trpí iluzí peněz. Podle nich by racionální pracovníci reagovali pouze na skutečné mzdy, tj. Na inflací očištěné mzdy. Avšak, jednou z charakteristických rysů moderní průmyslové ekonomiky je to, že se pracovníci nesetkávají s jejich zaměstnavateli na atomizovaném a dokonalém trhu. Pracují v složité kombinaci nedokonalých trhů, monopolů, monopsonů, odborových svazů a dalších institucí. V mnoha případech mohou mít pracovníci nedostatek vyjednávací síly, aby mohli jednat podle svých očekávání (bez ohledu na to, jak rozumná očekávání jsou) nebo na základě svého vnímání (bez ohledu na to, jestli trpí, nebo netrpí “iluzí” peněz). Není to tak, že vysoká inflace způsobuje nízkou nezaměstnanost (jak tomu je v teorii Miltona Friedmana) stejně tak tomu není naopak: Nízká nezaměstnanost zvyšuje pracovní vyjednávací sílu a umožňuje úspěšně prosazovat vyšší nominální mzdu. Za účelem ochrany zisku zvyšují zaměstnavatelé ceny.
Vestavěná inflace, je na tom podobně, není pouze záležitostí subjektivních "inflačních očekávání", ale také odráží skutečnost, že vysoká inflace může nabývat dynamiky a pokračovat dále, i po období, kdy byla zahájena. Toto se děje kvůli objektivní cenové (mzdové) spirále.
Jiní ekonomové, jako Jeffrey Herbener, tvrdí, že cena je tržně určená a konkurenceschopné firmy nemohou jednoduše zvýšit ceny. Odmítají Phillipsovu křivku a usuzují, že vliv nezaměstnanosti je jen malou částí mnohem většího inflačního obrazu která zahrnuje ceny surovin, polotovarů, náklady na získávání kapitálu, produktivitu pracovníků, půdu a další faktory.
Gordonův trojúhelníkový model
Robert J. Gordon z Northwestern University analyzoval Phillipsovu křivku, aby vytvořil takzvaný trojúhelníkový model, ve kterém je skutečná míra inflace určena součtem
- tahu poptávky nebo krátkodobou inflací Phillipsové křivky,
- tlakových nákladů nebo výkyvy dodávek (cost push or supply shocks,)
- vestavěné inflace.
Poslední odráží inflační očekávání a spirálu ceny / mzdy. Nabídkové šoky a změny vestavěné inflace jsou hlavními faktory, které posunují krátkodobou Phillipsovu křivku a změnu kompromisu, mezi vztahy uvedenými na křivce . V této teorii, inflační očekávání nejsou jedinými faktory, které mohou způsobit stagflaci. Během 70. let mohl být viníkem například strmý nárůst cen ropy.
Změny vestavěné inflace následují logiku částečného přizpůsobení, která stojí za většinou teorií NAIRU:
Nízká nezaměstnanost podporuje vysokou inflaci, jako u základní Phillipsovy křivky. Pokud však nezaměstnanost zůstane nízká a inflace zůstane vysoká po dlouhou dobu, jako v pozdních šedesátých letech v USA, urychlí se jak inflační očekávání, tak spirála ceny / mzdy. Toto posune krátkodobou Phillipsovu křivku směrem vzhůru a doprava tak, aby se zvýšila míra inflace u každé daně nezaměstnanosti. (Změnu můžeme vidět v B diagramu.)
Vysoká nezaměstnanost podporuje nízkou inflaci, opět jako u základní Phillipsovy křivky. Pokud však nezaměstnanost zůstane vysoká a inflace zůstane dlouhou dobu nízká, jako na počátku osmdesátých let v USA, inflační očekávání i spirála ceny / mzdy se zpomalí. Toto posune krátkodobou Phillipsovu křivku směrem dolů a doleva, takže se při každé míře nezaměstnanosti projeví menší inflace.
Mezi těmito dvěma leží NAIRU, kde Phillipsova křivka nemá žádnou inherentní tendenci k posunu, takže inflace je stabilní. Zdá se však, že existuje střední hodnota mezi "vysokým" a "nízkým", kde zůstává vestavěná inflace stabilní. Konce tohoto "neakcelerujícího inflačního rozpětí míry nezaměstnanosti" se v průběhu času mění.
Reference
V tomto článku byl použit překlad textu z článku Phillips Curve na anglické Wikipedii.
- Phillips, A. W. (1958). "The Relationship between Unemployment and the Rate of Change of Money Wages in the United Kingdom 1861-1957". Economica. 25 (100): 283–299.
- Samuelson, Paul A.; Solow, Robert M. (1960). "Analytical Aspects of Anti-Inflation Policy". American Economic Review. 50 (2): 177–194.
- Fisher, Irving (1973). "I discovered the Phillips curve: 'A statistical relation between unemployment and price changes'". Journal of Political Economy. The University of Chicago Press. 81 (2): 496–502.
- Forder, James (2014). Macroeconomics and the Phillips Curve Myth. Oxford University Press.ISBN 978-0-19-968365-9
- Domitrovic, Brain (10 October 2011). "The Economics Nobel Goes to Sargent & Sims: Attackers of the Phillips Curve". Forbes.com. Použito 12 October 2011.
- Oliver Hossfeld (2010) "US Money Demand, Monetary Overhang, and Inflation Prediction" Archivováno 19. 10. 2017 na Wayback Machine International Network for Economic Research working paper no. 2010.4
- Chang, R. (1997) "Is Low Unemployment Inflationary?" Federal Reserve Bank of Atlanta Economic Review 1Q97:4-13
- Jacob, Reed (2016). "AP Macroeconomics Review: Phillips Curve". APEconReview.com.
- Blanchard, Olivier (2000). Macroeconomics (Second ed.). Prentice Hall. pp. 149–55. ISBN 0-13-013306-X.
- Clarida, Richard; Galí, Jordi; Gertler, Mark (1999). "The science of monetary policy: a New-Keynesian perspective". Journal of Economic Literature. American Economic Association. 37 (4)
- Blanchard, Olivier; Galí, Jordi (2007). "Real Wage Rigidities and the New Keynesian Model". Journal of Money, Credit, and Banking. 39 (s1): 35–65.
- FIALOVÁ, Helena; FIALA, Jan. Malý ekonomický slovník s výkladem pojmů v češtině a v angličtině. Praha: A plus, 2006. ISBN 80-902514-8-X. S. 185–186.
- HLADÍK, René. Ekonomie: základní kurz (pro bakalářský stupeň vysokých škol). 2. vyd. Nové Město nad Metují: Reneco, 2005, 239 s. ISBN 80-865-6311-1.
- Forder, James (2010). "The historical place of the 'Friedman-Phelps' expectations critique". European Journal of the History of Economic Thought. 17 (3): 493–511.
- Galbács, Peter (2015). The Theory of New Classical Macroeconomics. A Positive Critique. Heidelberg/New York/Dordrecht/London: Springer. ISBN 978-3-319-17578-2
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu Phillipsova křivka na Wikimedia Commons
Obrázky, zvuky či videa k tématu Phillipsova křivka na Wikimedia Commons