Předzpracování obrazu

Abychom mohli lépe rozeznat jednotlivé degradující vlivy, zapíšeme rovnici ${\displaystyle z=D(u)\,}$ jako

${\displaystyle z(T(x,y))=(u*h)(x,y)+n(x,y)\,}$

kde ${\displaystyle T(x,y)\,}$ je operátor pro geometrické zkreslení a deformace(natočení obrázku, změna měřítka, posunutí), ${\displaystyle (u*h)(x,y)\,}$ značí konvoluci snímaného obrázku s impulzní odezvou zařízení, kterým snímáme(fotoaparát). Ideální snímací zařízení má impulzní funkci ${\displaystyle \delta (x)\,}$, tedy jednotkový pulz, ${\displaystyle n(x,y)\,}$značí šum v obraze. Tato rovnice a její řešení se nazývá Radiometric Inverze Problem a řešení se rozlišuje na případy:

• Impulzní odezva je známa - je znám typ odezvy a i její parametry
• Impulzní odezva je částečně známa - znám typ, ale neznám její parametry
• Impulzní odezva není vůbec známa

Nejdříve se zabývejme řešením, kdy není přítomen na fotce šum ani geometrická deformace, tedy ${\displaystyle n(x,y)=0\,}$ a ${\displaystyle T(x,y)~(x,y)\,}$. Řešíme tedy konvoluční rovnici ${\displaystyle z=u*h\,}$, která v diskrétní oblasti (obrázek je reprezentován jako matice intenzit) přechází v soustavu lineárních rovnic. Mějme výsledný obrázek ${\displaystyle z(x,y)\,}$ o rozměrech ${\displaystyle N\times N\,}$, dále známe impulzní odezvu ${\displaystyle h(x,y)\,}$ i její parametry ${\displaystyle (a,b,c)\,}$ tedy např. gaussova tvaru:

${\displaystyle \mathbf {h} ={\begin{pmatrix}b&a&b\\a&c&a\\b&a&b\end{pmatrix}}}$

Po provedení ${\displaystyle u*h\,}$ konvoluce dostáváme soustavu lineárních rovnic:

${\displaystyle \mathbb {Z} =\mathbb {H} \cdot \mathbb {U} \,}$

kde ${\displaystyle \mathbb {Z} }$ a ${\displaystyle \mathbb {U} \,}$ jsou vektory o rozměru ${\displaystyle N^{2}\,}$. Prvky obrázku v nich jsou seřazeny po řádcích:

${\displaystyle \mathbf {\mathbb {Z} =} \left({\begin{array}{c}z_{11}\\z_{12}\\\ldots \\z_{1N}\\z_{21}\\z_{22}\\\ldots \\\ldots \\z_{NN}\\\end{array}}\right),\mathbf {\mathbb {U} =} \left({\begin{array}{c}u_{11}\\u_{12}\\\ldots \\u_{1N}\\u_{21}\\u_{22}\\\ldots \\\ldots \\u_{NN}\\\end{array}}\right)}$

A matice ${\displaystyle \mathbf {\mathbb {H} } }$ (soustava lin. rovnic složená z výpočtu konvoluce) má rozměry ${\displaystyle N^{2}\times N^{2}\,}$ a následující tvar:

${\displaystyle \mathbf {\mathbb {H} } ={\begin{pmatrix}D&B&0&0&0&\dots &0\\B&D&B&0&0&\dots &0\\0&B&D&B&0&\dots &0\\\vdots &&\ddots &\ddots &\ddots &&\vdots \\\vdots &&&&&&\vdots \\\vdots &&&&\ddots &\ddots &\ddots \\0&0&0&0&B&D&B\\0&0&0&0&0&B&D\\\end{pmatrix}}}$, kde B a D jsou také matice rozměru ${\displaystyle N\times N\,}$ a tvaru:

${\displaystyle \mathbf {D} ={\begin{pmatrix}c&a&0&0&0&\dots &0\\a&c&a&0&0&\dots &0\\0&a&c&a&0&\dots &0\\\vdots &&\ddots &\ddots &\ddots &&\vdots \\\vdots &&&&&&\vdots \\0&0&0&0&a&c&a\\0&0&0&0&0&a&c\\\end{pmatrix}},\mathbf {B} ={\begin{pmatrix}a&b&0&0&0&\dots &0\\b&a&b&0&0&\dots &0\\0&b&a&b&0&\dots &0\\\vdots &&\ddots &\ddots &\ddots &&\vdots \\\vdots &&&&&&\vdots \\0&0&0&0&b&a&b\\0&0&0&0&0&b&a\\\end{pmatrix}}}$

Jak je vidět na první pohled, tak matice ${\displaystyle \mathbb {H} }$ i jednotlivé její „bloky“ (B, D) jsou tridiagonální. Tyto matice jsou řešitelné poměrně jednoduše a rychle. Výsledkem tedy bude vektor ${\displaystyle \mathbb {U} }$, což je požadovaný obrázek před konvolucí s ${\displaystyle h(x,y)\,}$.

Výpočet v obrazové oblasti je poměrně složitý (kvůli konvoluci), tak využijeme konvolučního teorému, který převádí konvoluci na násobení, což je nepoměrně rychlejší operace. Násobením je zde myšleno násobení (nebo dělení) po prvcích. Jestliže matice nemají stejný rozměr, tak se menší matice periodicky prodlouží na rozměr větší matice. Aplikujeme tedy Fourierovu transformaci na konvoluci ${\displaystyle u*h\,}$ a máme tedy:

${\displaystyle {\mathcal {F}}(z)={\mathcal {F}}(u*h)=U\cdot H\,}$

Z toho si lehce vyjádříme původní obrázek ${\displaystyle u}$, resp. jeho Fourierův obraz ${\displaystyle U}$.

${\displaystyle U={\frac {Z}{H}}\,}$

Pro obrazovou oblast tedy platí:

${\displaystyle {\mathcal {F}}^{-1}\left({\frac {Z}{H}}\right)\,}$

Tato metoda je používanější a nazývá se inverzní filtr ve frekvenční oblasti (anglicky: Inverse Filter in Fourier Domain).

Graf veličin N, H a N/H

V minulých odstavcích jsme předpokládali nulový šum, tedy ${\displaystyle n(x,y)=0\,}$ všude v obrázku. Nyní ho nezanedbáme a použijeme na rekonstrukci obrázku inverzní filtr. Vycházíme tedy z

${\displaystyle z(x,y)=(u*h)(x,y)+n(x,y)\,}$

Provedeme Fourierovu transformaci a vyjádříme si obrázek ${\displaystyle u(x,y)\,}$ před degradací.

${\displaystyle Z=U\cdot H+N\,}$,

${\displaystyle U={\frac {Z}{H}}-{\frac {N}{H}}\,}$.

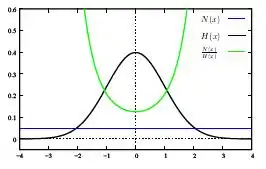
Z této rovnice je vidět, že jsme v předchozích metodách (pro případ zašuměného obrázku) zanedbali člen ${\displaystyle -{\frac {N}{H}}\,}$. Tento člen ale dosahuje obrovských hodnot, takže tyto metody dávají velmi špatné výsledky při použití u zašuměných obrázků. Jako impulzní odezvu mějme standardní gaussovu funkci (${\displaystyle =h(x,y)\,}$). Její Fourierova transformace je opět gaussova funkce dělená jejím rozptylem (${\displaystyle =H\,}$). Šum bereme libovolný, například takový, že jeho Fourierův obraz je konstantní funkce (ale není podmínkou, bereme jen pro jednoduchost). A protože gaussovka jde pro velké x k nule, tak její převrácená hodnota jde k nekonečnu a to násobené nějakým nenulovým šumem je zase velmi velké číslo (viz obrázek vpravo). Z toho plyne, že je při výpočtu zanedbán velmi významný člen. To je také důvod, proč se inverzní filtr moc nepoužívá. Místo něho se dá aplikovat na zašuměný obrázek Wienerův filtr, který dává o moc lepší výsledky.