Přechodový jev
Přechodový jev je fyzikální děj probíhající v časovém intervalu mezi dvěma ustálenými stavy. V ustáleném stavu se energie soustavy nemění (popř. se mění periodicky), v přechodovém stavu dochází ke změně energie soustavy.
Vznik jevu je podmíněn změnami energie v akumulačních prvcích obvodu (kondenzátory, cívky). Tyto změny nemohou proběhnout okamžitě, protože by vyžadovaly zdroj nekonečného výkonu. Charakter jevu závisí na druhu zapojených akumulačních součástek. Obsahuje-li obvod pouze jeden druh těchto součástek (tj. kromě odporu pouze kondenzátory nebo pouze cívky), nemůže dojít k vratné výměně energie a děj probíhá aperiodicky. Pokud však obvod obsahuje oba druhy akumulačních součástek, může za určitých podmínek dojít k tlumenému periodickému kmitání. Tyto obvody pak nazýváme oscilátory.
Přechodové jevy prvního řádu
V praxi rozeznáváme dva druhy obvodů s přechodovými jevy prvního řádu:
- Obvod RL
- Obvod RC
Přechodový jev v RL obvodu
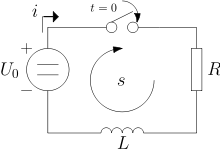
RL obvod je tvořen zdrojem napětí a sériovým zapojením ideálního odporu (rezistoru) a ideální cívky (induktoru). Po připojení ke zdroji stejnosměrného napětí začne obvodem procházet proud, který na cívce vytvoří magnetické pole, které však zatím nemá žádnou energii. To se však rychle mění, magnetické pole se zvětšuje a na cívce se začne indukovat napětí. Toto napětí je zpočátku stejně velké jako napětí zdroje, zatímco napětí na rezistoru je rovno nule. Postupně se však bude napětí na cívce snižovat a na rezistoru zvyšovat až bude v čase T obvodem protékat proud .
Celkové hodnoty v RL obvodu
- pro výpočet celkového napětí v obvodu
- pro výpočet okamžitého proudu v obvodu
- pro výpočet okamžitého napětí na rezistoru
- pro výpočet okamžitého napětí na cívce
Po odpojení obvodu od zdroje napětí se začne v cívce indukovat napětí opačné polarity, které způsobí zpomalení zániku magnetického pole. Směr toku proudu se nezmění. Energie magnetického pole cívky se přemění na rezistoru na energii tepelnou.
Okamžité hodnoty v RL obvodu
- pro výpočet okamžitého proudu v obvodu
- pro výpočet okamžitého napětí na rezistoru
- pro výpočet okamžitého napětí na cívce
Přičemž časovou konstantu τ vypočítáme (pro oba procesy) pomocí vztahu:
Přechodový jev v RC obvodu
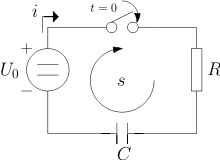
RC obvod je obdobně tvořen zdrojem napětí a sériovým zapojením ideálního odporu (rezistoru) a ideálního kondenzátoru (kapacitoru). Po připojení zdroje napětí bude obvodem procházet nejvyšší možný proud, který bude omezen pouze rezistorem . Nenabitý kondenzátor se tak bude zpočátku chovat jako zkrat. Čím více se však bude kondenzátor nabíjet (bude v něm vzrůstat nahromaděný náboj) a poroste jeho napětí (uc), tím menší proud bude procházet obvodem . Za dobu T tak bude obvodem procházet proud .
Odpojení RC obvodu


- pro výpočet celkového napětí v obvodu
- pro výpočet okamžitého proudu v obvodu
- pro výpočet okamžitého napětí na rezistoru
- pro výpočet okamžitého napětí na kondenzátoru
Po odpojení obvodu od zdroje napětí se začíná kondenzátor vybíjet (chová se jako zdroj). Elektrická energie, kterou kondenzátor vybije se v rezistoru přemění na energii tepelnou. Teoreticky se kondenzátor vybíjí nekonečně dlouhou dobu. V praxi se ale považuje za vybitý, pokud obvodem prochází již jen 5% maximálního proudu, což nastává za dobu 3τ.
Okamžité hodnoty v RC obvodu
- pro výpočet okamžitého proudu v obvodu
- pro výpočet okamžitého napětí na rezistoru
- pro výpočet okamžitého napětí na kondenzátoru
Přičemž časovou konstantu τ vypočítáme (pro oba procesy) pomocí vztahu:
Přechodové jevy druhého a vyššího řádu
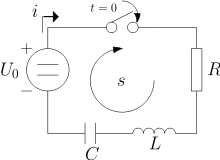
Přechodový jev 2. a vyššího řádu se liší pouze tím, že v obvodu jsou dva či více akumulačních prvků.
Přechodný jev 2. řádu
Při analýze je nutné definovat rovnici, která vychází ze smyčky s, tedy
Tuto rovnici je nutné zderivovat podle času t, dostáváme rovnici druhého řádu.
Nyní můžeme vytvořit charakteristickou rovnici, u které hledáme kořeny.
Pokud je
, pak řešením jsou 2 reálné kořeny a a děj je tzv. aperiodický.
, pak řešením jsou dva shodné reálné kořeny a děj je na tzv. mezi aperiodicity.
, pak řešením jsou 2 kořeny komplexně sdružené a děj je tzv. kmitavý.