Odhad vzdáleností
Odhad vzdáleností je praktická lidská dovednost, která se hodí zejména při jakémkoliv pobytu člověka ve volné přírodě. Jde také, mimo jiné, o tradiční součást skautské a vojenské praxe. Každý skaut i voják by měl umět odhadnout vzdálenosti od několika centimetrů až po několik set metrů. Zde je uvedeno několik základních metod, jak vzdálenosti a míry odhadovat.
Klasické odhady vzdáleností v přírodě
Pomocí hole nebo provázku
Na skautské holi by měl každý skaut mít vyznačené následující délky: 1, 5, 10, 50 a 100 centimetrů/palců, což mu usnadní hodně práce. Dále skauti v KPZ nosí provázek, který může mít uzlíky uvázané opět na vzdálenostech 1, 5, 10, 50 a 100 centimetrů a palců od konce.
Pomocí biometrických údajů
Pokud člověk nemá s sebou svoji hůl, nebo provázek s mírami, může se pokusit rozměry odhadnout pomocí rozměrů svého těla. Každý skaut by měl znát svoje míry (tj. kolik měří jeho palec, píď, sáh, krok, stopa atd.). Následující tabulka uvádí přibližné hodnoty pro dospělého člověka.
| Část těla | cm | palce |
|---|---|---|
| Kořen nehtu na ukazováku nebo šířka palce | 2,5 | 1 |
| Rozpětí mezi palcem a ukazovákem | 20,3 | 8 |
| Rozpětí mezi palcem a malíkem | 22,9 | 9 |
| Od zápěstí po loket nebo délka chodidla | 25,4 | 10 |
| Od lokte ke špičce ukazováku (tzv. loket) | 43,2 | 17 |
| Od středu čéšky kolena k podlaze | 45,7 | 18 |
| Krok | 75 | 18 |
Optické odhady
Ne všechny rozměry však lze změřit přímo, větší vzdálenosti se dají krokovat, ale občas člověk potřebuje jen základní odhad s přesností na 50 metrů, proto větší vzdálenosti odhadujeme, podle toho, jaké detaily jsme schopni rozeznat.
| co rozeznám | přibližná vzdálenost (m) |
|---|---|
| jasně viditelné oči, ústa | 50 |
| oči vypadají jen jako tečky | 100 |
| knoflíky a podrobnosti oblečení | 200 |
| obličej | 300 |
| pohyb nohou, směr chůze | 400 |
| barva oblečení | 500 |
| co rozeznám | přibližná vzdálenost (m) |
|---|---|
| listí na stromech | 200 |
| větší větve | 400 |
| telegrafní tyče, kmeny stromů | 1000 |
| osamělé stromy | 2000 |
| vrcholky kopců | 5000 |
Pozor: uvedené vzdálenosti jsou pouze orientační. Záleží na kvalitě vašeho zraku a také na počasí. Je-li hezké slunečné počasí, věci se zdají být blíže, je-li ošklivo, pak dále.
Pomocí zvuku
Vzdálenost je někdy také možné odhadnout podle zvuku. Vidíme-li například blesk, spočítáme sekundy mezi zábleskem a hromem, totéž platí pro umělé záblesky, které vznikají například pří výstřelech z palných zbraní. Počet sekund pak vynásobíme rychlostí zvuku a získáme odhad vzdálenosti v metrech. Zvuk se ve vzduchu šíří rychlostí přibližně 345 m/s, tedy přibližně 1/3 kilometru za sekundu – počet sekund můžeme vydělit 3 a získáme tak přibližnou vzdálenost v kilometrech (rychlost zvuku ve vzduchu je také mírně závislá na jeho teplotě, tlaku a vlhkosti).
Matematické odhady vzdáleností v přírodě
Tyto odhady výšky a vzdálenosti přes řeku či údolí se používají, když není možné použít standardní měřící přístroje, jako je pásmo, metr apod. Je však nutné umět trošku počítat. Uvádím zde nejznámější dva matematické odhady, které vycházejí z podobnosti trojúhelníků.
Výška
K velice přesnému odhadu výšky stromu či něčeho jiného vysokého (dům, rozhledna apod.) nám bude užitečná skautská hůl, jejíž výšku můžeme snadno změřit, a jeden pomocník.
Skautskou hůl zabodneme do země nebo ji necháme někomu podržet 9 metrů od stromu, který chceme měřit. Sami pak popojdeme o další 1 metr, přiložíme oko k zemi a podíváme se na špičku stromu přes hůl. Pomocník pak tak dlouho posouvá ruce po holi nahoru a dolů až bude oko, jeho ruka na holi a špička stromu v jedné přímce. Pak změř vzdálenost ruky pomocníka od země v milimetrech. Vynásobením této vzdálenosti desítkou dostaneme výšku stromu v centimetrech.
Vzdálenost přes řeku či údolí
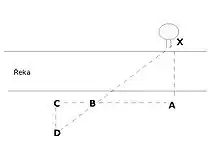
K určení šířky řeky, širokého příkopu nebo podobné díry nám výborně poslouží následující odhad.
Stoupneme si na břeh naproti nějakému orientačnímu bodu, např. stromu. Označme si pro přehlednost místo, kde stojíme A (viz obrázek), strom X. Z bodu A běž 60 m podél břehu řeky do bodu B, kde zarazíme do země skautskou hůl. Dále pokračujeme dalších 30 m do bodu C. I místo C si raději něčím označíme (postačí kámen). V bodě C vlevo v bok (tedy obrat o 90 stupňů od původní trasy) a nyní hledáme bod D. Bod D leží na spojnici bodu B a X. Vzdálenost mezi bodem D a C je polovinou vzdálenosti z bodu A do bodu X – šířky řeky.