Lineární kongruentní generátor

Lineární kongruentní generátor (anglicky Linear Congruential Generator, zkratka LCG) je jeden z nejstarších a nejjednodušších generátorů pseudonáhodných čísel.

Je definován vztahem:

${\displaystyle x_{i+1}=(ax_{i}+c)\ {\bmod {\ }}m\,}$,

kde operace mod znamená zbytek po celočíselném dělení, ${\displaystyle a}$, ${\displaystyle c}$ a ${\displaystyle m}$ jsou vhodně zvolené konstanty. Počáteční nastavení ${\displaystyle x_{0}}$ se nazývá random seed („náhodné semínko“). Generátor generuje celá čísla s rovnoměrným rozložením v rozsahu ${\displaystyle 0\leq x_{i}<m}$. Poněvadž je počet možných hodnot v tomto rozsahu omezen, začne se nejpozději po ${\displaystyle m}$ vygenerovaných číslech opakovat stejná posloupnost (tzv. perioda generátoru). Generátor bude mít plnou periodu (${\displaystyle m}$) právě tehdy, když:[1]

1. ${\displaystyle \,c}$ a ${\displaystyle \,m}$ jsou nesoudělná čísla,
2. ${\displaystyle \,a-1}$ je dělitelné všemi provočíselnými faktory ${\displaystyle \,m}$,
3. ${\displaystyle \,a-1}$ je násobek 4, jestliže ${\displaystyle \,m}$ je násobek 4.

9000 hodnot (3000 bodů) vygenerovaných lineárním konguentním generátorem při špatně zvolených konstantách a, c, m. Je patrné, že body zdaleka nevyplňují celou krychli, ale leží pouze v 15 rovnoběžných rovinách.

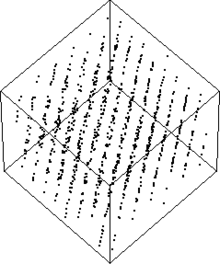
Větší problém, než je periodicita generátoru, lze u tohoto typu generátoru pozorovat při generování náhodných bodů v prostoru. V případě špatně zvolených hodnot ${\displaystyle a}$, ${\displaystyle c}$, ${\displaystyle m}$ leží vygenerované body v několika rovnoběžných rovinách, zatímco zbytek prostoru, který by měl být rovnoměrně zaplněn, je prázdný. Nechvalně se tak proslavil například generátor RANDU (${\displaystyle a=65539}$, ${\displaystyle c=0}$, ${\displaystyle m=2^{31}}$, ${\displaystyle x_{0}}$ je liché číslo) používaný okolo roku 1970.

Příklady konstant:

zdroj	m	a	c	výstup
Numerical Recipes	${\displaystyle 2^{32}}$	1 664 525	1 013 904 223
Borland C/C++	${\displaystyle 2^{32}}$	22 695 477	1	bity 30–16 v rand(), 30–0 v lrand()
glibc (GCC)	${\displaystyle 2^{32}}$	1 103 515 245	12 345	bity 30–0
ANSI C: Watcom, Digital Mars, CodeWarrior, IBM VisualAge C/C++	${\displaystyle 2^{32}}$	1 103 515 245	12 345	bity 30–16
Borland Delphi, Virtual Pascal	${\displaystyle 2^{32}}$	134 775 813	1	bity 63–32 ze (seed * L)
Microsoft Visual/Quick C/C++	${\displaystyle 2^{32}}$	214 013	2 531 011	bity 30–16
Apple CarbonLib (Park & Miller)	${\displaystyle 2^{32}-1}$	16 807	0