Hra života
Hra života nebo také život (anglicky Game of Life či pouze Life) je dvoustavový, dvourozměrný celulární automat[1], který svým chováním připomíná vývoj společenství živých organismů.[2] Odehrává se na matici buněk, jejíž stav předurčuje podobu hry v následujícím kroku. Uživatel pouze určí výchozí konfiguraci a dále již hra běží automaticky podle předem daných pravidel. Čas je ve hře diskrétní[3], při každém uplatnění pravidel se posune o jednotku. Hra života se od podobných celulárních automatů liší v pravidlech pro zrod nových buněk a jejich přežití. Kořeny hry života sahají do roku 1940, kdy maďarský matematik John von Neumann přišel s konceptem celulárních automatů. Hru života jako takovou však vymyslel až britský matematik John Horton Conway v roce 1970. V průběhu hry vznikají různé tvary, které se dělí do kategorií jako jsou zátiší, oscilátory, děla a další. Hra života je příkladem systému, kde z jednoduchých pravidel vzniká komplexní chování - objevují se zde tzv. emergentní struktury.

Herní svět
Dvourozměrná hrací plocha Hry života se znázorňuje jako čtvercová síť. Její políčka se nazývají buňky (proto název celulární neboli buněčný automat)[4]. Každá buňka může nabývat dvou stavů, může být živá či mrtvá.[2] Buňka sousedí s dalšími buňkami, se kterými se dotýká hranou (ortogonálně) či vrcholem (diagonálně) a tvoří tak Moorovo okolí. [3] Nový stav buňky určuje přechodová funkce podle stavu této buňky a jejího okolí v předchozím kroku.[3] Stav všech buněk se mění naráz.[2] Celulární automaty, které po vzoru Hry života splňují výše uvedené skutečnosti tvoří třídu celulárních automatů založených na Hře života (Life-like cellular automata).[4] Sestavení živých a neživých buněk na hrací ploše se říká konfigurace nebo vzor.[1] Jednotkou času je ve Hře života generace.[3] Jedna generace představuje jedno provedení přechodové funkce.[3] Podle toho, jaká pravidla pro změnu stavu buněk přechodová funkce uplatňuje, se hovoří o konkrétním názvu life-like celulárního automatu.[4]
Pravidla
Popis
Jako Hra života se označuje celulární automat jehož přechodová funkce používá množinu pravidel, kterou na počátku 70. let definoval britský matematik John Conway takto[5]:
- Každá živá buňka s méně než dvěma živými sousedy zemře.
- Každá živá buňka se dvěma nebo třemi živými sousedy zůstává žít.
- Každá živá buňka s více než třemi živými sousedy zemře.
- Každá mrtvá buňka s právě třemi živými sousedy oživne.
Tato konkrétní pravidla jsou označována jako S23/B3.[4] Čísla před lomítkem říkají kolik sousedů musí buňka mít, aby přežila, čísla za lomítkem říkají kolik sousedů potřebuje mrtvá buňka k ožití. Písmena jsou zkratky anglických výrazů to survive a to be born. Tato pravidla byla vybrána vědomě s cílem zajistit, aby populace živých buněk rostla nepředvídatelně.[5]
Konkrétně jde o splnění požadavků, že by:
- neměl existovat žádný počáteční vzor, pro který by šlo snadno dokázat, že populace může růst nade všechny meze[5],
- měly existovat počáteční vzory zdánlivě nade všechny meze rostoucí[5]
- a že by měl existovat takový počáteční vzor, který se určitou dobu vyvíjí než úplně vymizí, přejde do stabilní podoby anebo do oscilační fáze.[5]
Možných pravidel pro Life-like buněčné automaty je celkem 2^18.[3] Pro definici počtu buněk nutných k přežití či oživnutí lze totiž použít pro každou z nich celkem 9 možností (0-8 sousedů) a buňka se nachází ve dvou stavech. Při některých pravidlech všechny vzory vymizí, v některých dochází k explozivnímu růstu.[3]
Příklad
Obrázek znázorňuje vývoj vzoru v průběhu tří generací. Černě vybarvená buňka je ve stavu živém, bílá ve stavu neživém. Číslo uvnitř buňky označuje počet živých buněk v jejich okolí. Přechodová funkce se řídí pravidly S23/B3.
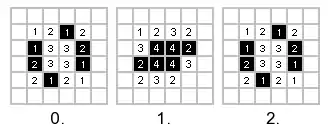
V nulté generaci se vlevo dole nachází živá buňka s právě jedním sousedem. Tato buňka po aplikaci pravidel zemře a v příští generaci se stane neživou. Vlevo a vpravo se nachází živé buňky se dvěma sousedy. Tyto buňky přežijí do příští generace. Čtyři neživé buňky uprostřed, které mají každá tři živé sousedy, v příští generaci ožijí. V první generaci se uprostřed nachází čtyři buňky každá se čtyřmi sousedy. Tyto buňky podle pravidel zemřou a v příštím kole budou neživé. Pravidla se uplatní i na ostatní buňky a výsledkem je generace 2. V tomto případě je druhá generace stejná jako nultá. Tento tvar spadá do skupiny oscilátorů s periodou dvě generace. Vzor se nazývá ropucha (toad).
Původ

Celulární automat vytvořil v roce 1940 John von Neumann za pomoci Stanislava Ulama ve snaze vytvořit sebereprodukující se stroj, tedy stroj schopný vytvářet své vlastní kopie.[6] Neumanův celulární automat měl podobu dvojrozměrné mřížky, kde se každá buňka mohla nacházet v jednom z 29 stavů.[3] Po čase zájem o celulární automaty trochu opadl, kvůli nedostatečnému výkonu tehdejší výpočetní techniky.[6] Novou vlnu zájmu o celulární automaty přinesla až Hra života na počátku sedmdesátých let.[6]
Hra života se na veřejnosti poprvé objevila v říjnu roku 1970 jako článek v rubrice Matematické hry spravované Martinem Gardnerem v časopise Scientific American. [5] Jejímu představení následoval dva roky trvající mezinárodní rozruch.[4] Martin Gardner přiznal, že její publikování způsobilo bezprecedentní čtenářský ohlas a že brzy bude potřeba vydat další článek ohledně technických principů, na který je Hra života založena.[3] Protože časopis Scientific American neposkytoval příznivcům Hry života dostatečný prostor pro publikaci nových objevů, založil Robert T. Wainwright v roce 1971 vlastní časopis s názvem LifeLine.[3] Časopis vycházel čtvrtletně a až do jeho ukončení v roce 1973 (kvůli osobním důvodům vydavatele) se těšil velkému zájmu čtenářů - zpočátku si jej předplácelo asi 150 zájemců, ke konci kolem 1000.[3]
Počáteční výzkum Hry života provázely dvě zásadní otázky.[3] Obě položil Conway. První z nich se objevila již v Gardnerově prvotním článku z října roku 1970.[5] Šlo o to zjistit, zda nějaký tvar může růst bez omezení. Jinými slovy, zda nějaká konfigurace s konečným počtem živých buněk může růst nad určitý konečný horní limit. Conway předpokládal, že taková konfigurace neexistuje a slíbil odměnu 50 dolarů tomu, kdo do konce roku jeho domněnku potvrdí či vyvrátí. Článek obsahoval i několik konceptuálních způsobů, jak Conwayův předpoklad vyvrátit. Jedním způsobem je najít takovou konfiguraci, která opakovaně vytváří pohybující se vzory. V článku je taková konfigurace označena jako dělo (gun). Další způsobem je vytvořit takovou konfiguraci, která se hýbe sama a zanechává za sebou stopu. Tato konfigurace je v článku označena jako kouřící vlak (puffer train). Cenu vyhrál R. William Gosper, když v listopadu téhož roku představil funkční dělo podle Conwayova popisu.[4] Po svém autorovi nese vzor název Gosperovo dělo na kluzáky (Gosper Glider Gun). Gosper později vyřešil problém i druhou metodou, když zkonstruoval první kouřící vlak (puffer train)[3].
Druhou zásadní otázku položil Conway v časopise Lifeline roku 1972.[3] Této otázce se také říká problém existence dědečka (The Grandfather Problem)[3] a Conway za její zodpovězení vypsal odměnu dalších 50 dolarů. Jde o to zjistit, jestli existuje taková konfigurace, která se vyskytuje pouze v druhé a už v žádné další generaci. Tato otázka nebyla dodnes zodpovězena.[zdroj?]
Mezi další dosud nevyřešené problémy patří dokázat, že existují vzory se všemi periodami (periody 19, 23, 34, 38, 41, 43 a 53 nejsou známé)[zdroj?], najít takový vzor, který vytváří více kopií sebe samého[zdroj?] a dokázat existenci zátiší, které mohou vzniknout pouze v nulté generaci[zdroj?].
Přehled tvarů
Vzory, které ve Hře života vznikají lze rozdělit do deseti hlavních kategorií. [7] Nadpis tvoří český překlad a anglický ekvivalent. U každé kategorie je jako příklad uvedeno několik často uváděných tvarů.
Zátiší (Still life)
Jako stabilní konfigurace se označuje vzor, který je svým vlastním rodičem.[1] Jako rodič vzoru se označuje přímý předchůdce.
Zátiší někdy označované také jako invariantní podoby (invariant forms)[4] je skupina tvarů, které se v průběhu hry nemění.[3] Jedná se o stabilní vzory složené z konečného počtu živých buněk.[1] Pro určování počtu zátiší o určitém množství živých buněk se používá užší definice, která přidává podmínku, že zátiší nesmí být možné rozdělit způsobem při kterém by jeho části zůstaly stabilní samostatně.[1] Vzory, které vyhovují první ale už ne druhé definici se nazývají pseudozátiší (pseudo still lifes).[1] Příkladem pseudozátiší je dvojblok na obrázku níže.
 |  |  |  |  |
| Blok (Block) | Včelín (Beehive) | Bochník (Loaf) | Loď (Boat) | Dvojblok (bi-block) |
Oscilátory (Oscillators)
Oscilátor je nestabilní konečný vzor, který je svým vlastním předchůdcem.[1] Předchůdcem se myslí jakýkoliv vzor, z něhož se daný vzor vyvinul za určitý počet generací.[1] Oscilátory periodicky přecházejí mezi konstantním počtem konfigurací.[4] U oscilátorů se sleduje periodicita. Oscilátory s periodou 2 postupně nabývají podoby jedné ze dvou možných konfigurací[4] a říká se jim alternátory.[3] První tři oscilátory na obrázcích mají periodu 2, pulzar má periodu 3.
 |  |  | |
| Blikač (Blinker) | Ropucha (Toad) | Maják (Beacon) | Pulzar (Pulsar) |
Děla
Jako dělo se označuje stacionární vzor, který do nekonečna opakovaně vytváří Posunovací se vzory nebo vidle.[1] Příkladem děla je křídelné dělo, které vypustí křídlo každých třicet generací.[4]
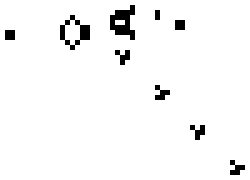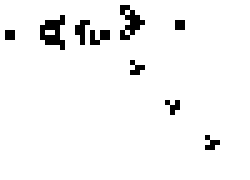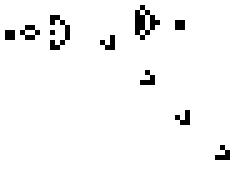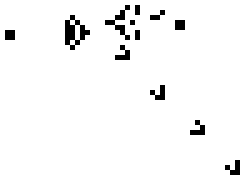
Posunovací se vzory
Posunovací se vzor je pohybující se vzor, který se v nezměněné podobě znovu objevuje po určitém počtu generací.[1] V nekonečném prostoru hry života není vzor nikdy periodický.[3] U posunovacích se vzorů se sleduje jejich rychlost, která je udávána jako zlomek rychlosti světla c.[1] Rychlost světla je definována jako jedna buňka za generaci a představuje největší rychlost, jakou se může ve Hře života objekt pohybovat.[1]
Nejznámějším případem posunovacího se vzoru je křídlo.[1] Jedná se o vzor složený z pěti živých buněk, které se nachází ve čtyřech fázích, které by se nebýt posunutí daly považovat na cyklus.[3] Pohybuje se diagonálně rychlostí c/4.[1]
 |  |
| Křídlo (Glider) | Lehká hvězdná loď (LWSS) |
Kuřáci (Puffers)
Kuřák je vzor, který se pohybuje jako hvězdná loď (starship) s tím, že za sebou nechává stopu.[1] První puffer objevil Bill Gosper v roce 1971.[3] Tento vzor se pohyboval rychlostí c/2 ortogonálně.[1] Obrázek ukazuje dva kuřáky. Nahoře je zobrazen Gosperův kouřící vlak, dole vzor nazývaný Blinker Puffer 1, jehož objevil Robert Wainwright v roce 1984.
Rajská zahrada (Garden of Eden)
Rajská zahrada nebo také sirotek (orphan) je taková konfigurace, která se může objevit pouze v nulté generaci.[1] O jejich existenci se vědělo dlouho před jejich praktickou realizací ve Hře života. Existencí této konfigurace se na počátku šedesátých let předpověděli Edward F. Moore a John Myhill.[4]
Moorův-Myrhillův teorém říká: pokud má nějaká konfigurace více než jednoho předka, tak existuje taková konfigurace, která žádného předka nemá a naopak.[4] Teorém se vysvětluje na následujícím příkladu.[4] Pokud se hrací plocha skládá z konečného množství buněk N a každá buňka se může nacházet ve dvou stavech, potom celkový počet možných konfigurací je 2^N v každé generaci. Pakliže jsou dvě různé konfigurace vytvoří v další generaci totožnou konfiguraci, pak přechodovou funkcí bylo vygenerováno pouze 2^N - 1 konfigurací a jedna konfigurace tedy nemá předchůdce.
První praktický vzor nalezl Roger Banks v roce 1971.[1] Tento vzor je na obrázku níže.

Metuzalémové (Methuselahs)
Jakýkoliv malý vzor, jehož stabilizace trvá dlouhou dobu.[1] R-pentomino se stabilizuje až po 1103 generacích, žalud po 5206 generacích a králíkům přechod do stabilního stavu trvá 17332 generací.
 |  |  |
| R-pentomino | Žalud (Acorn) | Králíci (Rabbits) |
Agary (Agars)
Agar je takový vzor, který pokrývá celou hrací plochu a je periodický jak v prostoru tak čase.[1]
 |  |
| Benátské rolety (Venetian blinds) | Chickenwire |
Pilové zuby (Sawtooths)
Konečný vzor, jehož populace roste bez omezení ale neroste do nekonečna přímo. Vždy po určité době růstu klesne na určitou konstantní hodnotu.[1]
První vzor, jehož graf populace v průběhu generací připomínal stále rostoucí zuby pily sestrojil Dean Hickerson v roce 1991.[7]
Pravidla celulárních automatů založených na Hře života
Life-like celulární automaty se rozlišují podle pravidel, která uplatňuje přechodová funkce. Existuje množství jiných pravidel než je původní S23/B3 tvořící Hru života. Tato pravidla tvoří další zajímavé tvary. První číslo před lomítkem je počet okolních buněk potřebných k přežití již živé buňce, druhé počet buněk na zrod. Pokud první číslo chybí, buňka vždy umře. Některá z těchto pravidel shrnuje následující tabulka.
| Pravidlo | Jméno | Popis |
|---|---|---|
| /2 | Semena | Chaotický vznik |
| /234 | Ubrousky | Krajkovité vzory |
| 012345678/3 | Vločky, nesmrtelné | Vločkovité vzory |
| 1/1 | Suky | |
| 12345/3 | Bludiště | Tvoří vzhled jako bludiště |
| 125/36 | 2x2 | Pokud je vzor složen z bloků 2×2, pokračuje ve vývoji stejnou formou. Má hodně oscilátorů a lodí |
| 1357/1357 | Nahrazovač | Nahrazovač Edwarda Fredkina: každý vzor je jednou nahrazen několikanásobnými kopiemi sebe sama |
| 1358/357 | Améba | Dobře vyvážený poměr mezi životem a smrtí; tvoří tvary s chaotickými vnitřky a rychle pohybujícími hranicemi. Její lodě[nedostupný zdroj] |
| 23/3 | Game of Life | Velmi komplexní chování |
| 23/36 | HighLife | Podobný Game of Life |
| 2345/45678 | Města za zdmi | Tvoří oblasti s pevnými hranicemi, pohyb je pouze uvnitř |
| 235678/3678 | Skvrny | Vzor se rychle stabilizuje, poté už jen slabě osciluje |
| 235678/378 | Srážlivý | Vzor má sklon se rozvíjet právě opačně než velmi podobné pravidlo Skvrn |
| 238/357 | Pseudo life | Vývoj vzoru je podobný Game of Life, ale málo vzorů z Life funguje s tímto pravidlem |
| 245/368 | Pohyb | Náhodné vzory mají sklon se stabilizovat, ale má mnoho přirozeně vyvinutých a navrhovaných lodí |
| 34/34 | 34 Life | Vytvořena původně jako stabilní alternativa pro Life, dokud počítačové simulace neukázaly, že velké vzory mají sklon explodovat. Má hodně malých oscilátorů[nedostupný zdroj] a lodí |
| 34678/3678 | Day & Night | Symetricky obrácený. Má navržené vzory s velmi komplexním chováním |
| 4567/345 | Přizpůsobení | Tvoří trvalé kosočtvercové vzory s částečně vyplněným vnitřkem |
| 45678/3 | Korál | Vzory připomínají pomalu se tvořící korálové textury |
| 5/345 | Long life | Zkoumána Andrewem Trevorrowem, má oscilátory s velmi dlouhou periodou |
| 5678/35678 | Kosoaméba | Formuje se do velkých kosočtvercových tvarů s chaoticky oscilujícími hranicemi. |
Příklad algoritmu
n=100; % počet řádků a sloupců
t=100; % čas
U=rand(n); % matice s náhodnými elementy
p=0.25; % počáteční poměr
A=(U<p); % počáteční matice se kterou se hraje
B=zeros(n); % pomocná matice, kam zapisuji další iterační stavy
for i=1:t
for x=2:n-1
for y=2:n-1
okoli=A(x-1,y-1)+A(x-1,y)+A(x-1,y+1)+A(x,y-1)+A(x,y+1)+A(x+1,y-1)+A(x+1,y)+A(x+1,y+1);
if A(x,y)==1 % živá buňka
if okoli==2 | okoli==3
B(x,y)=1; % zůstane
else
B(x,y)=0; % zahyne
end
else % mrtvá buňka
if okoli==3
B(x,y)=1; % ožije
else
B(x,y)=0; % neožije
end
end
end
end
imshow(B)
pause(.01)
A=B; % před dalším krokem je nutno matici A aktualizovat
end
Reference
- SILVER, Steven. Life Lexicon [online]. 28.2.2006 [cit. 2011-01-25]. Dostupné v archivu pořízeném dne 26-05-2013. (anglicky)
- GARDNER, Martin. Mathematical Games: The fantastic combinations of John Conway.. Scientific American. 1970, čís. 223, s. 120–123. [<http://www.fpga-faq.org/sb-metal_hold/CD_08/lifepatt.pdf> Dostupné online]. (anglicky)[nedostupný zdroj]
- ADAMATZKY, Andrew. Game of Life Cellular Automata. London: Springer-Verlag, 2010. 573 s. ISBN 978-1-84996-216-2. (anglicky)
- SCHIFF, Joel L. Cellular automata: A Discrete View of The World. New Jersey: John Wiley & Sons, Inc, 2008. 252 s. ISBN 978-0-470-16879-0. (anglicky)
- BERLEKAMP, Elwyn R.; CONWAY, John H.; GUY, Richard K. Winning Ways for Your Mathematical Plays. Wellesley: A K Peters, 2004. 967 s. ISBN 1-56881-144-6. (anglicky)
- HUSÁKOVÁ, Martina. Celulární automaty: Znalostní technologie III materiál pro podporu studia. [s.l.]: [s.n.], 2007. 14 s. (česky)
- Life Wiki [online]. [cit. 2011-01-25]. Dostupné online. (anglicky)
Online ukázka - applet
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu Hra života na Wikimedia Commons
Obrázky, zvuky či videa k tématu Hra života na Wikimedia Commons - (česky) Český Java applet pro online simulace
- (slovensky) Slovenské prostředí pro spouštění simulací online[nedostupný zdroj]
- (anglicky) Prostředí pro spouštění simulací online
- (anglicky) Diskusní fórum zaměřené na Hru života
- (anglicky) Rozcestník na čísla časopisu Lifeline
- (anglicky) Conway's game of life implementation. (Silverlight)
- (anglicky) Game of Life on JavaScript