Houghova transformace

Klasická Houghova transformace slouží pro detekci přímek v obraze. Používá se ve strojovém vidění; dlouho byla nejužívanější technikou pro detekci čar na silnici pro autonomní a částečně autonomní vozidla (v současné době se od této transformace upouští a používají se techniky rychlejší (LSD, EDlines)). Houghova transformace dokáže sama o sobě najít pouze přímky – pakliže je třeba najít úsečky, je potřeba aplikovat další kroky.

V běžných případech pracuje transformace nad černo-bílým (bez stupňů šedi, tj. binárním) obrázkem.

Prostor parametrů

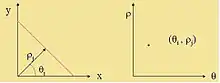
Transformace je založená na skutečnosti, že každá přímka v rovině x, y lze jednoznačně popsat dvojicí parametrů (r,σ), tedy vzdáleností od středu souřadnicového systému a úhlem od osy x.

Rovnice přímky v takovém tvaru je

x cos(σ)+y sin(σ)=r

Rovině se souřadnicovým systémem vymezeným osami (r,σ) se říká prostor parametrů.

Protože je přímka jednoznačně určena dvojicí (r,σ), zobrazí se každá přímka v (x,y) do (r,σ) jako jeden bod (viz obrázek) a naopak – bod v (r,σ) lze zobrazit jako přímku v (x,y).

Pro každý bod v (x,y) lze jednoduše najít množinu přímek, které tímto bodem procházejí. Je to množina (r,σ), splňujících uvedenou rovnici (x cos(σ)+y sin(σ)=r), když za (x,y) dosadíme souřadnice zkoumaného bodu.

Je zřejmé, že takováto množina splňující uvedenou rovnici bude mít v (r,σ) tvar sinusovky.

Pro každý nalezený (bílý) bod v (x,y) zobrazíme množinu přímek, které jím mohou procházet jako sinusovku do (r,σ).

Předpokládejme dále, že v (x,y) existují body ležící na přímce. Výše uvedeným postupem dokážeme pro každý bod vykreslit v (r,σ) množinu přímek, které jím mohou procházet. Přímku, která prochází všemi, můžeme tedy logicky najít jako průnik těchto množin.

Průniky sinusovek (množin), značící nalezenou přímku.

Tento průnik odpovídá v (r,σ) jednomu bodu, který je přímo parametrickým vyjádřením odpovídající přímky.