Hippokrates z Chiu
Hippokrates z Chiu, řecky Ἱπποκράτης ὁ Χῖος byl starořecký geometr a matematik z 5. století př. n. l.
| Hippokrates z Chiu | |
|---|---|
 | |
| Narození | 470 př. n. l. Chios |
| Úmrtí | 410 př. n. l. (ve věku 59–60 let) |
| Povolání | matematik, astronom a filozof |
 multimediální obsah na Commons | |
| Některá data mohou pocházet z datové položky. | |
Život
Podle tradice byl Hippokrates obchodník, jehož zboží ukradli piráti, a tak šel do Athén, aby se domohl spravedlnosti. To se mu příliš nezdařilo, ale začal v Athénách navštěvovat přednášky o matematice a posléze geometrii.
Aristoteles však vyprávěl jiný příběh, tvrdil, že Hippokrates nebyl okraden, ale byl napálen celníky v Byzanci. Aristoteles tím chtěl ukázat, že i když někdo může být dobrý teoretik a myslitel, nemusí být schopný zvládnout běžné záležitosti života, takže je otázkou, nakolik je jeho příběh historicky hodnověrný.
Dílo
V geometrii je považován za klíčového předchůdce Eukleidova. Stejně jako později Eukleidés, shrnul Hippokratés soudobé geometrické poznatky v knize Základy (Stoicheia). Ta se téměř celá ztratila, informace o Hippokratově geometrii čerpáme především od jeho následovníků Prokla (asi 410–485) a Simplicia z Cilicia, kteří Hippokrata spojují především s řešením kvadratury kruhu (úkol převést daný kruh na čtverec se stejnou plochou). Zachoval se jediný autentický zlomek Hippokratových Základů, a ten je věnovaný tzv. měsíčkům (meniskům). Z tohoto fragmentu můžeme soudit, že Hippokrates byl první, kdo formuloval zásady měření v oblasti křivek.
Hippokratovy měsíčky
Hippokratovy měsíčky jsou zelené plochy na následujícím obrázku a Hippokrates tvrdí, že tyto zelené měsíčky mají stejnou plochu jako červeně ohraničený trojúhelník o stranách a, b, c.
Hippokrates vyšel z Pythagorovy věty a2 + b2 = c2:
Vynásobením Pythagorovy věty konstantou π/8 vznikne:
π/8.a2 + π/8.b2 = π/8.c2
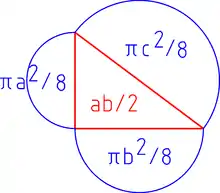
Kde se vzala konstanta π/8?
Obsah kruhu je πr2, kde r je poloměr kruhu. Půlkruh je polovina, πr2/2.
Když se místo poloměru dosadí průměr r=d/2, pak půlkruh má plochu πd2/8. Půlkruh se tedy liší od čtverce násobkem π/8.
Nyní se tento obrazec rozdělí na dva díly - modrý a žlutozelený - a ty se od sebe odečtou. Žlutozelený polokruh nad odvěsnou je vymezen Thaletovou kružnicí.
minus 
rovná se
Aritmeticky je to jednoduché:
[π/8.a2 + π/8.b2 + ab/2] - [π/8.c2] = [ab/2]
A to mělo být dokázáno.
Měsíčky, nazývané též Hippokratovy měsíčky, jsou obecně plochy omezené dvěma kruhovými oblouky, které mají stejný obsah jako nějaký mnohoúhelník (zejména trojúhelník nebo lichoběžník).
Ottův slovník naučný definuje Hippokratovy měsíčky takto: "Hippokratovy měsíčky (lunulae Hippocratis) povstávají, opíšeme-li polokruhy nad odvěsnami pravoúhlého trojúhelníka do polokruhu vepsaného, i jest součet takto vzniklých měsíčků roven ploskému obsahu pravoúhlého trojúhelníka. Důkaz Hippokratův vyžadoval jakési zvšeobecnění věty Pythagorovy, totiž: Jsou-li strany trojúhelníka pravoúhlého stejnolehlými podstavami, na nichž spočívají mnohoúhelníky podobné: rovná se ploský obsah mnohoúhelníka na přeponě součtu ploských obsahů mnohoúhelníků na odvěsnách."[1]
Protože Hippokrates svým objevem ukázal, že je možné zkonstruovat čtverec, jehož plocha se rovná ploše měsíčku, zdálo se logické, že zdánlivě podobný problém kvadratury kruhu by neměl být tak obtížný a část řecké geometrie se na něj upnula, což jí ovšem zavedlo do slepé uličky - problém není euklidovsky řešitelný.
Odkazy
Externí odkazy
- Obrázky, zvuky či videa k tématu Hippokrates z Chiu na Wikimedia Commons
- Heslo v encyklopedii Amapro Archivováno 5. 3. 2016 na Wayback Machine
- Heslo v Britannice
- Heslo z Dictionary of Scientific Biography na Encyclopedia.com
