Hertzův tlak
Hertzův tlak (neboli styčný tlak ev. kontaktní pnutí) je tlak, který vzniká v místě vzájemného silového působení dvou těles s definovaným zakřivením povrchu. Svůj název nese po německém fyzikovi Heinrichu Hertzovi, který řešení této úlohy (formulované jako tzv. Hertzův model) publikoval v roce 1882.
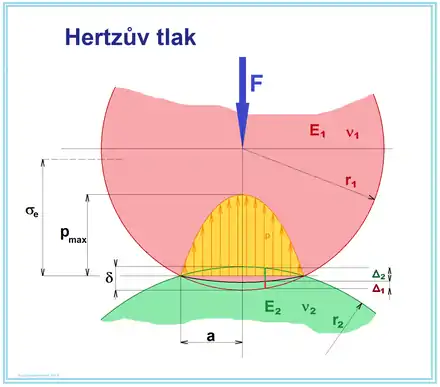
Hertzův model
Hertzův model je založen na těchto předpokladech:
- Rozměr stykové plošky je podstatně menší než poloměry křivosti dotýkajících se těles
- Všechna vzniklá napětí jsou menší, než meze pružnosti těles
- Na stykové ploše je nulové tření i adheze
Výpočet
V obecném zadání figurují parametry dotýkajících se těles (těleso 1 a těleso 2):
- hlavní křivosti – menší a větší (kde ), což jsou navzájem kolmé největší a nejmenší křivosti ve stykovém bodě.
U těles vydutých (střed křivosti plochy leží mimo těleso) má křivost zápornou hodnotu . - úhel natočení – úhel mezi rovinami křivosti a
Pokud je jedním z těles koule, pak je a - moduly pružnosti materiálů těles – a
- Poissonova čísla materiálů těles – a
Obecné řešení
Odvození velikosti tlaku ve styčné ploše vychází z deformačních podmínek tuhých těles, kdy se nejprve stanoví velikost a tvar stykové plochy, jimž je obecně elipsa. Průběh tlaku na stykové ploše je parabolický (pokud nepřekročí mez pružnosti jednoho z materiálů), což vychází z průběhu deformace radiusu povrchu. Maximální tlak vyvozený silou se nachází uprostřed dotykové elipsy a má velikost[1]
- , kde a jsou rozměry poloos dotykové elipsy:
- V těchto formulích je hodnota činitelů
pro a - Konstanty a jsou definovány v tabulce podle úhlového parametru , který se vypočte jako
- V těchto formulích je hodnota činitelů
Konstanty pro výpočet poloos dotykové elipsy[1] 20° 30° 35° 40° 45° 50° 55° 60° 65° 70° 75° 80° 85° 90° 3,778 2,731 2,397 2,136 1,926 1,754 1,611 1,486 1,378 1,284 1,202 1,128 1,061 1,00 0,408 0,493 0,530 0,567 0,604 0,641 0,678 0,717 0,759 0,802 0,846 0,893 0,944 1,00
Případy se zcela obecným zadáním jsou v praxi velice ojedinělé a přibližuje se k nim například odvalování kuličky v rádiusové drážce valivého ložiska.
Typické případy
V typických případech figurují obvykle koule, válec a rovina.
Pro zjednodušení lze brát
koule – koule
V tomto případě je styková plocha kruhová ( a ) a její poloměr je
Maximální tlak pak je:
Přiblížení středů koulí je
koule – rovina
Rovina je v podstatě koule o nekonečném poloměru, tudíž a pak je poloměr stykové plochy
Maximální tlak pak je:
V případě shodných materiálů koule i podložky () dostaneme vztahy:
- ; ;
Pro kalenou ocelovou kouli na kalené ocelové rovině lze použít pro určení dovolené zátěže při maximálním dovoleném tlaku
přibližný vzoreček: pro F v [N] a d v [cm].[1]
rovnoběžné válce
Styková plocha má tvar obdélníka o šířce b, takže
- , kde je zatížení vztažené na jednotku délky
Maximální tlak pak je:
válec – rovina
V tomto případě platí
Maximální tlak pak je:
V případě shodných materiálů válce i podložky () dostaneme vztahy:
- ; ;
Při předběžném návrhu mostních ložisek lze použít zjednodušený vzoreček pro q v [N/cm] a d v [cm].[1]
Odlišné vzorce
V literatuře se vyskytují i poněkud odlišné vzorce. Je to jednak použitím jiné úpravy konstant a jednak použitím
tzv. redukovaného modulu pružnosti
a tzv. ekvivalentního rádiusu
Jiné modely kontaktního pnutí
Zohledňují vliv adheze:
- Bradleyův model
- Model pružného kontaktu Johnson-Kendall-Roberts (JKR)
- Model pružného kontaktu Derjaguin-Muller-Toporov (DMT)
- Taborův parametr – spojuje modely JKR a DMT
- Model pružného kontaktu Maugis-Dugdale
- Model Carpick-Ogletree-Salmeron (COS)
– dle odstavce „Adhesive contact between elastic bodies“ v článku „Contact mechanics“ na anglické Wikipedii
Reference
- HÖSCHL, Cyril. PRUŽNOST A PEVNOST VE STROJNICTVÍ. Praha: STNL, 1971. 376 s. S. 267.