Geoid

Geoid je fyzikální model povrchu Země při střední hladině světových oceánů. Je definován jako ekvipotenciální plocha vůči gravitaci, to jest plocha se stejnou úrovní tíhového potenciálu, na kterou je vektor tíhového zrychlení kolmý. Hodnota W₀ geopotenciálu, kterou přijala IAU, je 62636856 m²s⁻².[1]

Mapa zvlnění geoidu v metrech (na základě gravitačního modelu EGM96 a referencích WGS84 elipsoidu)

1. Oceán
2. Referenční elipsoid
3. Místní linie olovnice
4. Kontinent
5. Geoid

Trojrozměrná vizualizace zvlnění geoidu v gravitačních jednotkách

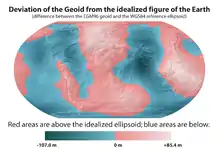
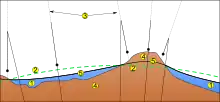
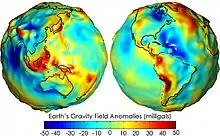
Geoid je vlastně reprezentovaný ekvipotenciální plochou, která co možná nejvíce přimyká ke střední klidové hladině oceánu, ale také myšleně prochází i pod povrchem Země.

Geoid, jako matematické těleso aproximující zemský povrch, pochází z roku 1871 z dílny německého matematika a fyzika Johanna Benedikta Listinga. V průběhu času dospěli vědci zdárně ke třem základním definicím geiodu:

• Definice geografická – geoid je těleso, které atmosféra odděluje od střední klidové hladiny moří a oceánů
• Definice geofyzikální – geoid je tvořen ekvipotenciální plochou, která se co nejvíce přimyká střední klidové hladině moří a oceánů
• Definice geodetická – geoid je tvořen ekvipotenciální plochou, která se co nejvíce přimyká střední klidové hladině moří a oceánů a zároveň prochází daným nulovým bodem

Geoid se vůči referenčnímu zemskému elipsoidu může lišit až o ± 100 m. Pro popis geoidu je často používána jeho sférická harmonická reprezentace. Nejlepší současná sada koeficientů pro tuto reprezentaci je EGM96 (Earth Gravity Model 1996), sestavený na základě mezinárodního projektu, vedeného National Geospatial-Intelligence Agency.

Geoid určuje na zemském povrchu nadmořskou výšku v daném výškovém systému. Pro současné poziční/navigační systémy se jako referenční zemský elipsoid používá WGS84.