Cavalieriův princip

Cavalieriův princip neboli Cavalieriho princip je poznatek stereometrie používaný při výpočtu objemu těles a pojmenovaný po svém objeviteli, italském matematikovi Bonaventurovi Cavalierim (1598 – 1647). Cavalieriho princip ve třírozměrném případě říká, že tělesa se stejně velkými podstavami a výškami mají stejný objem, pokud mají řezy rovnoběžné s podstavami a vedené ve stejné vzdálenosti od podstav stejné obsahy. Ve dvourozměrném případě Cavalieriův princip tvrdí rovnost obsahu dvou rovinných obrazců, pokud úsečky rovnoběžné s osou souřadné soustavy, které je protínají ve shodné výšce, mají vždy stejnou délku.

Cavalieriho princip použitý pro výpočet objemu koule

Z moderního pohledu jde o důsledek Fubiniho věty integrálního počtu.

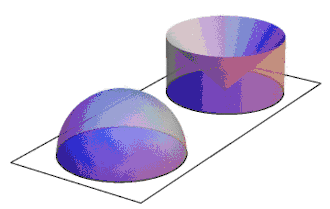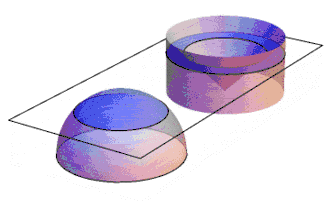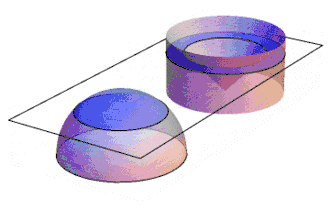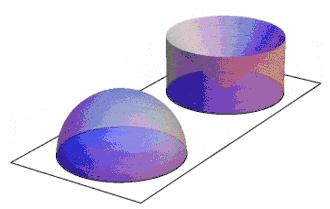
Cavalieriův princip lze použít například pro výpočet objemu koule elementárními prostředky, jak je znázorněno na animaci. Nejdříve ukážeme, že polokoule o poloměru R má stejný objem jako válec s podstavou o poloměru R a o výšce R, z něhož je vyříznut obrácený kužel tak, jak ukazuje vyobrazení. Podstavy i výšky obou těles se rovnají a rovnají se i obsahy řezů v kterékoli výšce v nad podstavou. U polokoule je řez kruhový, jehož poloměr je podle Pythagorovy věty ${\displaystyle r={\sqrt {R^{2}-v^{2}}},}$ a má tedy plochu ${\displaystyle S_{k}=\pi r^{2}=\pi (R^{2}-v^{2})}$. Řez vyříznutého válce je mezikruží s plochou ${\displaystyle S_{v}=\pi R^{2}-\pi v^{2}=\pi (R^{2}-v^{2})}$, a to je stejné jako obsah řezu polokoule ${\displaystyle S_{k}}$. Platí tedy předpoklady Cavalieriho principu, a to znamená, že obě tělesa na obrázku mají stejný objem. Objem vyříznutého válce je rozdílem objemu válce a objemu kužele: ${\displaystyle V_{v}=\pi R^{3}-{\frac {\pi }{3}}R^{3}={\frac {2\pi }{3}}R^{3}.}$ Objem celé koule je tedy dvojnásobný: ${\displaystyle V_{koule}={\frac {4\pi }{3}}R^{3},}$ což je správný vzorec pro objem koule.