Booleova logika
Booleova logika se zabývá logickými operacemi "*" (konjunkce, značená též AND, & nebo ), "+" (disjunkce, značena též OR, "|", "." nebo ) a "NOT()" (negace, značena též pruhem nad částí výrazu) na množině hodnot { 0, 1 }. Jejím rozšířením je pak Booleova algebra.
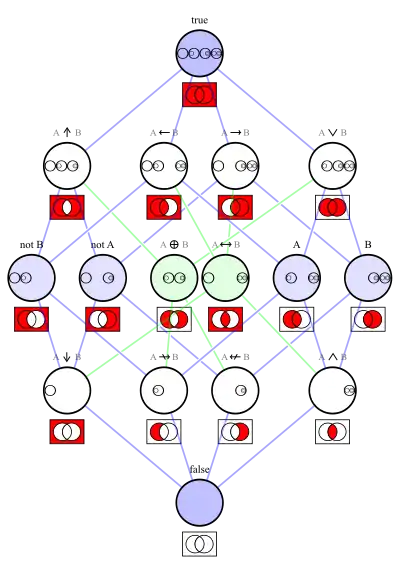
Definice logických funkcí
| A | ID | NOT | |
|---|---|---|---|
| 0 | 0 | 1 | |
| 1 | 1 | 0 |
| A | B | OR | NOR | AND | NAND | XOR | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | ||||
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | ||||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | ||||
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
Negace
NOT – vrací opačnou hodnotu, než měl vstup. Platí:
- NOT( 0 ) = 1, komplement
- NOT( 1 ) = 0, komplement
- A = NOT ( NOT(A) ), involuce
Disjunkce
OR – vrací součet hodnot vstupů. Platí:
- 0 + 1 = 1
- 1 + A = 1, agresivita, omezenost
- 0 + A = A, neutralita, omezenost
- A + A = A, idempotence
- A + B = B + A, komutativita
- A + NOT(A) = 1, komplement
Konjunkce
AND – vrací součin hodnot vstupů. Platí:
- 0 * 1 = 0
- 1 * A = A, neutralita, omezenost
- 0 * A = 0, agresivita, omezenost
- A * A = A, idempotence
- A * B = B * A, komutativita
- A * NOT(A) = 0, komplement
Základní pravidla
Párová pravidla platí i po vzájemné záměně "+" za "*", zde jsou tyto operace vzájemně symetrické.
Absorpce
- A*(A+B) = A, protože (A+B) jen rozšiřuje už platný a užší fakt A, takže zbytečné.
- A+(A*B) = A, protože (A*B) jen zužuje už platný a širší fakt A, takže zbytečné.
Asociativita
- (A+B)+C = A+(B+C)
- (A*B)*C = A*(B*C)
Distributivita
- A*(B+C) = AB+AC
- A+(B*C) = (A+B)*(A+C), protože A+AB+AC+BC = A+A*(B+C)+BC = (A+A*D)+E = A+E, (substituce, pak absorpce závorky)
Neutrálnost 0 a 1
- A+0 = A
- A*1 = A
Idempotence
- A+A = A
- A*A = A
De Morganovy zákony
Logický součet a součin lze vyjádřit jeden pomocí druhého, při použití negace.
De Morganovy zákony tedy definují negace logického součtu a součinu:
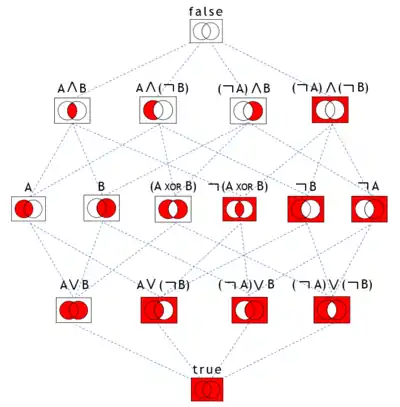
Implikace
NOR – Buď při splněném předpokladu A vrací B, nebo z nesplněného předpokladu vyplývá cokoli a vrací 1:
- A B = NOT(A) + B = NOT( A*NOT(B) )
Ekvivalence
EQ – porovnává shodnost hodnot všech vstupů:
- A B = A*B + NOT(A)*NOT(B) = (A+NOT(B)) * (NOT(A)+B)
Exkluzivní disjunkce
XOR – porovnává unikátnost hodnoty každého vstupu:
- A XOR B = A*NOT(B) + B*NOT(A)
XOR versus NEQ
Obecně jsou XOR a nonekvivalence rozdílné funkce, ale pro dvě dvouhodnotové proměnné dále platí:
- ( A XOR B ) = NOT( A B )
nebo jinak,
- XOR(A,B) = NOT(EQ(A,B))
Související články
- Karnaughova mapa
- Vytýkání