Archimédův axiom
Archimédův axiom nebo Archimédova vlastnost je princip pojmenovaný podle starořeckého matematika Archiméda, který říká, že pro dvě libovolná kladná čísla existuje přirozené číslo takové, že . Prakticky se tedy jedná o vlastnost, že v dané algebraické struktuře není žádný nekonečný prvek.
Vlastnost je možné pojmout jako axiom, kterým je spoludefinována struktura, na které se dále pracuje (tak jej použil například David Hilbert ve svém axiomatickém zavedení geometrie), nebo se může jednat o vlastnost, která je dokázána na základě jiných axiomů.
Struktura, která splňuje Archimédovu vlastnost, se nazývá archimédovská, mluví se tedy o archimédovské grupě nebo o archimédovském tělese. V závislosti na struktuře existují i ekvivalentní formulace archimédovské vlastnosti, například pro obory integrity obsahující celá čísla: „Ke každému kladnému prvku lze nalézti alespoň jedno přirozené číslo takové, že .“[1]
Dějiny a název
Sám Archimédés tento axiom zmínil ve svém pojednání O kouli a válci vzniklém kolem roku 225 př. n. l., pravidlo bylo ovšem známé už Eudoxovi z Knidu o dvě století dříve a přibližně půl století před Archimédem jej zmiňuje ve svých Základech jako 4. definici páté knihy Eukleidés, který zároveň také dává v 16. větě třetí knihy dává příklad veličiny, která toto pravidlo nesplňuje.
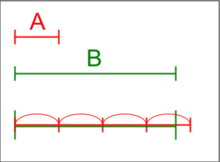
V rámci starořecké matematiky ovšem často nebývala tvrzení vyjadřována přímo v číslech, ale geometricky délkou úseček. Archimédův axiom touto řečí říká, že pokud máme zadány dvě úsečky, pak je můžeme položit na stejnou přímku do stejného počátečního bodu a pokud budeme k jedné z nich přikládat její další kopie, tak nakonec získáme úsečku delší než je druhá.
Po Archimédovi tento princip pojmenoval rakouský matematik Otto Stolz.
Odkazy
Reference
- KOŘÍNEK, Vladimír. Základy algebry. Praha: Nakladatelství Československé akademie věd, 1956. S. 73.
Externí odkazy
 Obrázky, zvuky či videa k tématu Archimédův axiom na Wikimedia Commons
Obrázky, zvuky či videa k tématu Archimédův axiom na Wikimedia Commons