Izomorfizmus grafov
Izomorfizmus grafov je relácia ekvivalencie na triede všetkých grafov. Ak majú byť grafy G a G’ izomorfné, musia mať všetky grafové charakteristiky rovnaké (počet vrcholov, počet hrán, valenčné postupnosti, počet komponentov atď.).
Ak sa ukáže, že grafy majú niektoré z týchto charakteristík odlišné, nemôžu byť izomorfné.
Izomorfizmus grafov G a G'
Definícia:
Graf G = (V,H) je izomorfný s grafom G’ = (V,H‘), ak existuje vzájomne jednoznačné zobrazenie (bijektívne) f : V ↔ V‘ také, že pre každú dvojicu vrcholov u,v ∈ V platí:
- {u, v} ∈ H práve vtedy, keď { f(u), f(v) } ∈ H‘.
Izomorfizmus digrafov G a G‘
Definícia:
Digraf G = (V,H) je izomorfný s digrafom G‘ = (V,H‘ ), ak existuje vzájomne jednoznačné zobrazenie f : V ↔ V‘ také, že pre každú dvojicu vrcholov u, v ∈ V platí:
- (u,v) ∈ H práve vtedy, keď (f(u),f(v)) ∈ H‘.
Jediný možný spôsob ako dokázať, že grafy alebo digrafy G a G’ (s vlastnosťami izomorfizmu z definície) sú izomorfné je vyskúšať všetky vzájomne jednoznačné zobrazenia f, ktorých je n!, kde n = |V|.
Problémy grafového izomorfizmu
- Zostrojiť všeobecný algoritmus, ktorý by pre ľubovoľné dva grafy rozhodol, či sú izomorfné alebo nie.
- Dokázať, že žiaden taký algoritmus neexistuje.
Konkrétny príklad izomorfizmu grafov
Majme grafy G1 a G2 :
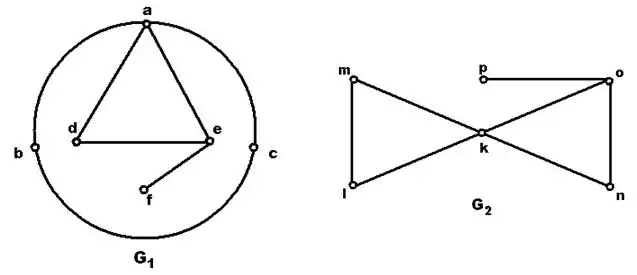
V tomto prípade existuje zobrazenie f, kde k = f(a), l = f(b), m= f(c), n= f(d), o = f(e), p= f(f).
Izomorfizmus f sa môže zapísať v tvare dvojriadkovej tabuľky, v ktorej v prvom riadku sú vrcholy grafu G1 a v druhom ich obrazy zobrazenia f :
Z definície izomorfizmu grafov vyplýva, že pre dva izomorfné grafy G a G’ platí |H| = |H’| a |V| = |V’|
Splnenie týchto podmienok ale nezaručuje, že grafy sú izomorfné. Na dokázanie izomorfizmu grafov by pomohol algoritmus, ktorý však stále nebol objavený.