Ekliptikálna sústava súradníc
Ekliptikálna sústava súradníc je jedna zo sústav súradníc používaných v astronómii.
Centrom ekliptikálnej sústavy súradníc môže byť stred Zeme alebo Slnka. Môže byť implementovaný v sférických alebo karteziánskych súradniciach.[1]
Pri ekliptikálnej sústave súradníc tvorí základnú rovinu rovina dráhy Zeme okolo Slnka, ktorá pretína nebeskú sféru v rovine ekliptiky, s pólmi severný pól ekliptiky Pe, a južný pól ekliptiky P'e. Druhou základnou kružnicou je kružnica na sfére, prechádzajúca pólmi ekliptiky a jarným bodom. Jarný bod je jedným z priesečníkov rovníka s ekliptikou. Druhým priesečníkom je jesenný bod Ω . Tieto priesečníky sa nazývajú body rovnodennosti, ekvinokciálne body. Sklon ekliptiky k rovníku ε = 23°27'. V týchto bodoch vystupuje Slnko pri svojej zdanlivej dráhe na sfére na jar (okolo 21.3.) nad rovník a na jeseň (okolo 23.9.) zostupuje pod rovník.
Sférické súradnice
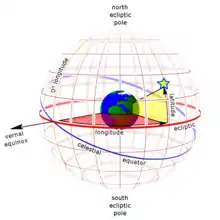
Jednou z dvoch súradníc ekliptikálnej sústavy súradníc je uhlová vzdialenosť telesa od ekliptiky meraná pozdĺž šírkovej kružnice telesa (hviezdy) od ekliptiky po hviezdu, a to kladne smerom k severnému pólu ekliptiky, záporne smerom k južnému pólu ekliptiky. Vyjadruje sa v stupňoch od 0° do 90° a nazýva sa ekliptikálna šírka β. Druhá súradnica vyjadruje uhlovú vzdialenosť šírkovej kružnice hviezdy od nulovej šírkovej kružnice prechádzajúcej jarným bodom. Je to ekliptikálna dĺžka λ hviezdy, meria sa v stupňoch od 0° do 360° od jarného bodu v smere zdanlivého pohybu Slnka po ekliptike (kladný smer). Ekliptikálne súradnice λ β spolu so sklonom ekliptiky s jednoznačne určujú polohu nebeského telesa vzhľadom na ekliptiku.
Ekliptikálna sústava súradníc sa používa najmä na určenie polôh telies slnečnej sústavy, ktorých dráhy ležia blízko ekliptiky. V dôsledku sekulárnych a periodických zmien vyvolaných precesiou a nutáciou sa polohy základných rovín rovníkovej a ekliptikálnej sústavy súradníc menia v priestore; posúvajú sa tým základné roviny a nulový bod (ν) na určovanie súradníc. Preto je potrebné k určeným súradniciam hviezdy uviesť, na akú polohu základných rovín a nulového bodu sa vzťahujú, treba udať epochu alebo ekvinokcium (napr. začiatok roka 1985,0).
| Sférické | Pravouhlé | |||
|---|---|---|---|---|
| dĺžka | šírka | vzdialenosť | ||
| Geocentrické | λ | β | Δ | |
| Heliocentrické | l | b | r | x, y, z |
pri geocentrických súradniciach sú symboly x, y, z vyhradené pre rovníkový systém. | ||||
Ekliptikálne súradnice λ β sú spojené s pravouhlými súradnicami x, y, z vzťahmi:
- x = r cos(β) cos(λ)
- y = r cos(β) sin(λ)
- z = r sin(β).
pričom rovina xy je rovinou ekliptiky, os x mieri k jarnému bodu a os z k severnému pólu ekliptiky. Na základe toho možno ľahko nájsť transformačné vzťahy medzi ekliptikálnymi a rovníkovými súradnicami, keď sa začiatok obidvoch sústav súradníc položí do jedného bodu (paralelným posunutím sa smer súradnicových osí nemení) a uhol medzi jednotlivými osami sa vyjadrí pomocou sklonu ekliptiky k rovníku ε (osi x sú totožné, smerujú do jarného bodu). Rovnako na základe riešenia sférického trojuholníka s vrcholmi svetový pól P, pól ekliptiky Pe a hviezda H, so stranami 90-δ, 90-β, ε a uhlami 90-λ, a 90+α možno použitím viet sférickej trigonometrie nájsť transformačné vzťahy medzi ekliptikálnymi a rovníkovými súradnicami, napr. ekliptikálne súradnice zo známych rovníkových (ekvatoreálnych) súradníc
- cos(β) cos(λ) = cos(δ) cos(α),
- cos(β) sin(λ) = cos(δ) sin(α) cos(ε) + sin(δ) sin(ε) ,
- sin(β) = sin(δ) cos (ε) - cos(δ) sin(α) sin(ε),
alebo naopak: nájsť rovníkové súradnice hviezdy, keď sú známe jej ekliptikálne súradnice
- cos(δ) cos(α) = cos(β) cos(λ),
- cos(δ) sin(α) = cos(β) sin(λ) cos(ε) + sin(β) sin(ε) ,
- sin(δ) = cos(β) sin(λ) sin(ε) + sin(β) cos(ε).
Pravouhlé súradnice
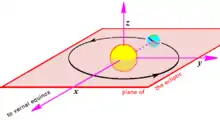
Karteziánsky variant ekliptických heliocentrických súradníc sa často používa pri orbitálnych výpočtoch a simuláciách. Má svoj stred v strede Slnka (alebo v barycentre Slnečnej sústavy), základná rovina je ekliptická rovina a os x smerom k jarnej rovnodennosti.
x = r cos(b) cos(l)
y = r cos(b) sin(l)
z = r sin(b).
Referencie
- Astronomical Almanac 1961. [s.l.] : [s.n.]. Dostupné online.
Zdroje
![]()
Tento článok je čiastočný preklad článku na Ecliptic coordinate system anglickej Wikipédii.