Časopriestor
Časopriestor alebo priestoročas je štvorrozmerný priestor zjednocujúci trojrozmerný fyzikálny priestor a čas. Body časopriestoru zodpovedajú bodovým udalostiam. Vnímanie času a priestoru ako nezávislých pojmov je závislé od pozorovateľa, ale časopriestor je od pozorovateľa nezávislý a tvorí základný rámec pre možnosť realizácie fyzikálnych zákonov nezávislých od vzťažnej sústavy vo vesmíre.
Časopriestor zaviedol Herman Minskowski v rokoch 1907 – 1908 (Einsteinov profesor matematiky).
Vlastnosti časopriestoru
Pri opise pohybu musíme zaznamenať nielen polohu, ale aj čas, zaznamenanej udalosti. Záznam o každej udalosti sa skladá vždy zo štyroch čísel, kde tri z nich udávajú polohu udalosti v priestore a jeden údaj udáva čas jej nastatia. Túto skutočnosť môžeme povedať aj inými slovami:
„všetky objekty aj my sa pohybujeme nielen v priestore, ale aj v čase“.
Alebo by sme mohli povedať skrátene v časopriestore. Všetky udalosti, dianie okolo nás, ale aj vo vesmíre sa odohráva v „aréne“ nazývanej časopriestor.
Na prvý pohľad by sa mohlo zdať, že takáto myšlienka dávať dokopy priestor a čas, len tým, že sme vymysleli akurát nový skrátený názov, neprinesie nič nového. Ukázalo sa však, že v relativite je to jedna z kľúčových myšlienok. Navyše v teórii relativity (v špeciálnej, ale aj všeobecnej) je dokonca nevyhnutné uvažovať vždy dianie v rámci časopriestoru, nikdy nie osobitne v priestore a osobitne v čase.
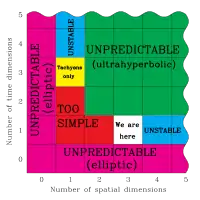
Vodorovná os: počet priestorových dimenzií
Zvislá os: počet časových dimenzií
UNPREDICTABLE: Správanie okolia sa nedá predpovedať zo znalosti príslušných parciálnych derivácií – spracúvanie informácií je nemožné
TOO SIMPLE: Vesmír má príliš jednoduchú geometriu – napríklad jednotlivé nervy sa nemôžu „obísť“, ale pretínajú sa. Tiež problémy s existenciou gravitačnej interakcie
TACHYONS ONLY: Rýchlosť svetla je najnižšou možnou rýchlosťou šírenia hmoty – skladá sa teda len z tachyónov
UNSTABLE: Obežné dráhy (elektrónov, planét, hviezd atď.) alebo samotné protóny sú nestabilné
We are here (náš vesmír): má práve také matematické a fyzikálne vlastnosti, že poskytuje najbohatšie prostredie pre život
Fine-tuned universe
Na výnimočnosť nastavenia dimenzionality nášho časopriestoru (tri priestorové a jedna časová dimenzia) upozornili niekoľkí autori. Súčasné aj rozpracované fyzikálne teórie sa pri makroskopickom popise nášho vesmíru zhodujú na tomto počte.[2] Tento problém bol skúmaný z fyzikálneho aj čisto matematického hľadiska. Iné počty makroskopických dimenzií vedú k vesmírom, v ktorých buď neexistuje stabilita dráh planét či stavebných blokov hmoty, alebo sú len veľmi jednoduché.[1]
Výpočet
Výpočet vzdialenosti bodov v priestore
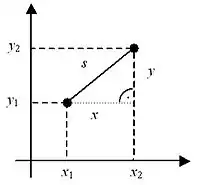
Ak je vzdialenosť medzi bodmi A a B je , resp. (pozri obr.), potom podľa Pytagorovej vety v dvojrozmernom priestore bude táto vzdialenosť:
Ak by ľubovoľný iný pozorovateľ použil svoje súradnice (označme ich s čiarkou) a vypočítal by:
potom
Obdobný vzorec platí aj pre trojrozmerný priestor.
Výpočet vzdialenosti medzi udalosťami
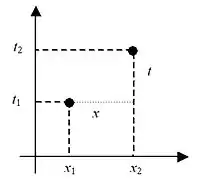
Aj medzi dvoma udalosťami (bodmi v priestoročase), existuje istý druh vzdialenosti. Udalosti v reálnom svete sú však odelené nielen v priestore ale aj v čase. Vo výpočte vzdialenosti medzi udalosťami vystupuje aj čas, aj priestor – priestoročasový interval.
Na obrázku sú znázornené udalosti A a B, ktoré sa líšia o , resp. o . Priestoročasový Interval vypočítame:
Tento vzorec je pre vzdialenosť danú Pytagorovou vetou veľmi podobný výpočtu vzdialenosti medzi dvoma bodmi. Ak ľubovoľný iný pozorovateľ použije svoje súradnice (označme ich s čiarkou) a výpočíta , dostane aj ten istý výsledok. Interval je pre všetkých pozorovateľov rovnaký, nemení sa, je invariantom:
Z nemennosti tohto intervalu vidíme okamžite prekvapujúci dôsledok – jednu z najväcších inovácii a zmien v našom chápaní času. Ak sú pre dvoch pozorovateľov rôzne priestorové vzdialenosti a medzi danými udalosťami, musia byť rôzne aj doby a medzi ich nastatiami (pričom je konštantná rýchlosť svetla ). Inak by sa interval nezachoval. Inými slovami čas nebeží rovnako pre všetkých pozorovateľov.
Pozri aj
Referencie
- Tegmark, Max.: "On the dimensionality of spacetime". Classical and Quantum Gravity 14 (4): L69–L75. 1997 http://space.mit.edu/home/tegmark/dimensions.pdf
- Barrow J. D., Tipler F. J.: The Anthropic Cosmological Principle. Oxford: Clarendon Press, 1986