Průběh signálu

Fourierova řada umožňuje rozklad libovolného periodického průběhu na součet (často nekonečného počtu) funkcí sinus a kosinus. Dokonce i neperiodické tvary vln s konečnou energií lze rozložit na součet sinusoid pomocí Fourierovy transformace. Pro rozklad funkce použít libovolný systém funkcí, které tvoří ortogonální bázi.

Pomocí osciloskopu lze zobrazit reprezentace vln jako opakující se obrázek na obrazovce. Existují také programy pro osobní počítače, které zobrazují tvary vln, z nichž lze získat vizuální představu, jak vypadá záznam určitého zvuku. Příliš malá nebo velká výška vlny znamená příliš malou nebo velkou hlasitost. Z toto příkladu vyplývá, že křivka reprezentující tvar vlny je ovlivněna jak vstupním signálem, tak podmínkami, za kterých byl zaznamenán.[1]

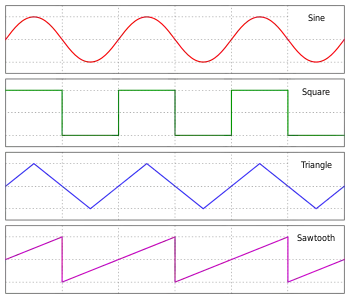
K nejčastějším příkladům periodických vln patří následující průběhy, kde ${\displaystyle t}$ je čas, ${\displaystyle \lambda }$ je vlnová délka, ${\displaystyle a}$ je amplituda a ${\displaystyle \phi }$ je fáze:

• Sinusoida ${\displaystyle (t,\lambda ,\phi )=\sin {\frac {2\pi t-\phi }{\lambda }}}$. Okamžitá hodnota je sinus času.
• Obdélníkový průběh ${\displaystyle (t,\lambda ,\phi )={\begin{cases}a,&(t-\phi ){\bmod {\lambda }}<s\\-a,&{\text{jinak}}\end{cases}}}$. Kde s je střída. Vlny tohoto tvaru se často používají pro reprezentaci digitální informace. Obdélníková vlna konstantní periody obsahuje pouze liché harmonické, jejichž amplituda se snižuje o 6 dB každou oktávu.
• Trojúhelníkový průběh ${\displaystyle (t,\lambda ,\phi )={\frac {2a}{\pi }}\arcsin \sin {\frac {2\pi t-\phi }{\lambda }}}$. Obsahuje liché harmonické, jejichž amplituda se snižuje o 12 dB každou oktávu.
• Pilovitý průběh ${\displaystyle (t,\lambda ,\phi )={\frac {2a}{\pi }}\arctan \tan {\frac {2\pi t-\phi }{2\lambda }}}$. Průběh připomíná asymetrické zuby pily. Tento průběh signálu se používal v časových základnách pro řízení zobrazovačů s vakuovými obrazovkami. Také se používá jako výchozí signál pro subtraktivní syntézu, protože pilovitá vlna konstantní period obsahuje liché i sudé harmonické, jejichž amplituda se snižuje o 6 dB každou oktávu.

Jiné tvary vln se obvykle nazývají složené tvary vln a často mohou být popsány jako složení několika sinusových vln nebo jiných bázových funkcí.