Styčník

Styčník neboli styčný bod soustavy[1] je bod či uzel, ve kterém jsou spojeny dva nebo více prutů konstrukce. V praxi není vzhledem k rozměrům průřezů prutů většinou možné jejich dovedení do jediného bodu a styčníkem je pak označován teoretický průnik prodloužených střednic stýkajících se prutů. Podle počtu připojených prutů označujeme styčníky jako dvojnásobné, trojnásobné, atd. V případě, že je uvažován styčník v rovinné konstrukci, přísluší mu 3 stupně volnosti (dva posuny a jedno natočení/pootočení), v prostoru pak 6 stupňů volnosti (tři posuny a tři natočení).[2][1] Ve styčnících může působit zatížení.

Příklady značení styčníků v prutové/rámové konstrukci: A - Tuhý styčník (vetknutí), B - Kloubový styčník, C - Tuhý styčník ( rámový styčník), D - kloubový pružný styčník (podpora, podepření), E - Posuvný tuhý styčník (podpora, podepření), F - Volný konec
Příklad realizace kloubového styčníku (kloubová vazba) - Nádraží Ostrava-Svinov
Příklad realizace kloubového styčníku (kloubová vazba) - Sopoty, Polsko

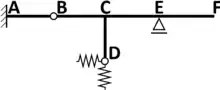
Kloubový styčník

Pokud je ve styčníku umožněno volné vzájemné natočení prutů, nazýváme ho kloubovým styčníkem. Pro teoretické vyšetřování sil působících v konstrukcích je v kloubovém styčníku zaveden zjednodušující předpoklad nulového kloubového tření a nulových vůli v kloubu (tzv. ideální nebo dokonalý kloubový styčník), který se také nazývá ideální kloub. Tento předpoklad zajišťuje ve styčníku nulovou hodnotu ohybového momentu[2] a také poměrně jednoduchý výpočet vnitřních statických účinků.

Kloubové styčníky mohou být volné (nejsou podepřeny, tj. nemají další vazbu) nebo vázané (jsou podepřeny, tj. mají další vazbu - podporu).

Tuhý styčník

V opačném případě pevného spojení prutů neumožňujícího jejich vzájemné volné pootočení hovoříme o tuhém styčníku. V případě, že není umožněno žádné teoretické natočení, jde o dokonale (absolutně) tuhý styčník nazývaný také jako rigidní styčník . Toto spojení prutů zajišťuje přenesení ohybového momentu a ostatních vnitřních statických účinků. Někdy je označován také jako jako rámový styčník. Příkladem tuhého styčníku je:

  • vetknutí
  • bezkloubové spojení dvou nosníků nebo prutů (např. rohové spojení v rámech)
Reálný styčník v lidském těle - anatomie kostí kolenního kloubu (articulatio genus)[3]

Pružný styčník

Jeho zavedení je motivováno přiblížením se reálné situaci.

Ve skutečnosti nemůže být tuhý styčník nikdy dokonale tuhý a také kloubový styčník nemůže mít dokonalý kloub. V podstatě téměř vždy jsou v pružném styčníku umožněny alespoň nějaké deformace (např. minimální natočení nebo posunutí). Velikost těchto deformací jsou závislé na tuhosti styčníku, která nabývá odpovídajících hodnot v závislosti na vlastnostech materiálů, průřezů prutů a vazeb.[2]

V mnoha případech, z konstrukčních důvodů, jsou v těchto styčnících umístěny pružiny a také umožněno pohyblivé spojení s vůlemi např. v kinematických mechanismech.

Volný konec

Volný konec, resp. začátek, prutu či nosníku se také označuje jako styčník.

Další informace

Styčníky lze také používat v mechanismech či v biomechanice při stanovení statiky, kinematiky a dynamiky pohybu segmentů těla a jeho částí.

Síly ve styčnících lze řešit jednoduše dle teorie 1. řádu nebo složitěji dle přesnější teorie 2. řádu či nejsložitěji a nejpřesněji dle teorie velkých deformací.

Odkazy

Reference
  1. O.Novák, J.Hořejší a kolektiv, Statika stavebních konstrukcí, Technický průvodce 4, SNTL, Praha 1972, str. 142,260
  2. Jaroslav Kadlčák, Jiří Kytýr, Statika stavebních konstrukcí I., VUTIUM, Brno 1998, str. 160,227,289
  3. FRYDRÝŠEK, Karel. Biomechanika 1. 1. vyd. Ostrava, Czech Republic,: VSB – Technical University of Ostrava, Faculty of Mechanical Engineering, Department of Applied Mechanics, 2019. 461. s. ISBN 978-80-248-4263-9.

Související články
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.