ROC křivka

ROC křivka (z anglického Receiver Operating Characteristic, operační charakteristika přijímače) je graf, který popisuje kvalitu binárního klasifikátoru v závislosti na nastavení jeho klasifikačního prahu.

Příklad několika ROC křivek v jednom grafu

Binárním klasifikátorem se rozumí zařízení (nebo člověk) odhadující zařazení nějakých objektů nebo případů do dvou skupin, obecně označovaných jako pozitivní a negativní. Přitom se předpokládá, že objekty jsou charakterizovány nějakou vlastností (proměnnou) vyjádřenou číslem a že klasifikátor zařazuje do pozitivní skupiny právě ty, u kterých hodnota této proměnné přesáhne stanovený klasifikační práh (což je nějaké pevně dané číslo). Příkladem binárního klasifikátoru může být bankéř, který na základě kreditního skóre nějaké osoby rozhoduje, zda jí lze (pozitivní) nebo nelze (negativní) úspěšně poskytnout úvěr. Klasifikátor na základě takového postupu může buď objekt zařadit správně, anebo se může dopustit chyby; navíc záleží i na tom, zda případ je, nebo není ve skutečnosti pozitivní. Lze tak rozlišit čtyři případy: 1. skutečný pozitivní (true positive, jejich počet se označuje TP; odpovídá situaci, kdy bankéř poskytne úvěr a klient ho řádně splatí), 2. skutečný negativní (true negative, TN; bankéř odmítne klienta, který by úvěr nesplatil), 3. falešný pozitivní čili falešný poplach (false positive, FP; poskytnutí úvěru klientovi, který peníze bance nevrátí) a 4. falešný negativní (false negative, FN; klient nedostane úvěr, i když by ho řádně splácel).

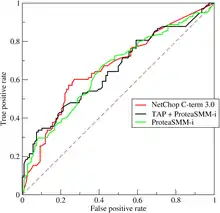
Na základě uvedených počtů lze odhadnout pravděpodobnost detekce (true positive rate), označovanou také jako senzitivita, jako TPR = TP / počet pozitivních = TP / (TP + FN), a pravděpodobnost falešného poplachu (false positive rate) jako FPR = FP / počet negativních = FP / (FP + TN). ROC křivka vynáší FPR na ose x a TPR na ose y pro všechny možné klasifikační prahy. Obě souřadnice klesají, když klasifikační práh roste: čím vyšší je klasifikační práh, tím méně případů klasifikujeme jako pozitivní, a tím také klesá senzitivita i pravděpodobnost falešného poplachu, až nakonec obě čísla klesají k nule. Naopak s klesajícím prahem se obě hodnoty blíží k jedničce. ROC křivky proto propojují bod (0, 0) a bod (1, 1). V případě, že proměnná, na jejímž základě se klasifikátor rozhoduje, příliš nesouvisí s tím, zda je zkoumaný případ pozitivní nebo negativní, se bude ROC křivka podobat úsečce spojující tyto dva body – nebude výrazně zakřivená. Naopak pokud proměnná obsahuje podstatnou informaci o pozitivitě nebo negativitě zkoumaných případů a klasifikační práh je nastaven správně, bude odpovídající bod na ROC křivce ležet v blízkosti „optimálního“ bodu (0, 1), v němž nedochází k žádným falešným poplachům a všechny pozitivní objekty jsou odhaleny. Čím tedy je ROC křivka zakřivenější ve směru vzhůru, tím víc klasifikační proměnná obsahuje informace o zařazení objektů a tím je její použití pro danou klasifikační úlohu vhodnější. Jako souhrnné hodnocení klasifikační schopnosti proměnné se proto často používá plocha pod ROC křivkou.

ROC křivky vznikly za druhé světové války při zkoumání schopností nově vynalezených radarů správně detekovat nepřátelská letadla. Postupně se rozšířily do psychologie, medicíny a dalších oborů, dnes se využívají velmi široce ve všech oblastech, kde se provádí klasifikace nějakých objektů na základě dat.