Příčinková čára

Příčinková čára je označení grafického znázornění průběhu určité statické veličiny, pořadnice η udává relativní velikost veličiny v daném průřezu v závislosti na působení pohybující se bezrozměrné jednotkové síly F = 1 [-].[1][2] Na rozdíl od grafu průběhu vnitřních sil vyjadřují sílu v pouze jednom bodě a příslušné pořadnice vyjadřují polohu pohyblivého zatížení. Mezi sledované veličiny mohou patřit reakce, ohybové momenty, posouvající síla i průhyby, jelikož je působící síla bezrozměrná, mají příčinkové síly vnitřních sil jednotku [-], ohybové momenty mají jednotku metr.

Průběh příčinkové čáry reakce v podpoře A pro staticky neurčitou konstrukci – spojitý nosník

Znázornění principu příčinkové čáry: pohybující se síla, graf p.č. ohybového momentu a posouvající síly

Příčinkové čáry pro různé statické veličiny

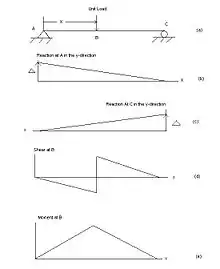
Teorie příčinkových čar je postavena na Bettiho teorému. Příčinkové čáry mohou být stanoveny buď z definice – pro každou polohu zatěžující síly se vyšetří hodnota statické veličiny v požadovaném bodě, nebo kinematicky (Müller-Breslauův princip) – dojde k fiktivnímu uvolnění vazby či vložení kloubu a konstrukci je udělen deformační impuls, průběh příčinkové čáry pak odpovídá tvaru deformované konstrukce.[1] Na staticky určité konstrukci mají tvar přímých (lomených) čar, na staticky neurčité konstrukci jsou čáry zakřivené.[1] Pokud se ale na staticky neurčité konstrukci nachází staticky určitá část (konzola, vložené prosté pole), má příčinková čára v tomto úseku lineární průběh.

Příčinkové čáry se využívají hlavně pro návrh mostů, pásových dopravníků a jeřábových drah – konstrukcí, kde se proměnné zatížení po konstrukci pohybuje.[1] Příčinkové čáry tak slouží pro vyšetření nejnepříznivější polohy pohyblivého zatížení, konkrétně se používá Winklerovo kritérium či kritérium max max M (rozšířené Winklerovo kritérium).[1]