Narozeninový problém

Graf s křivkou přibližné pravděpodobnosti, že alespoň dva lidé sdílejí narozeniny v dané skupině lidí.

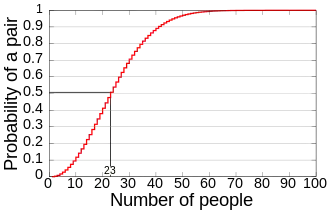
Pro výpočet pravděpodobnosti, že v místnosti s n lidmi alespoň dva mají narozeniny ve stejný den, budeme předpokládat rovnoměrné rozdělení narozenin během roku (tj. budeme ignorovat přestupné roky, dvojčata atd.)

Je jednodušší nejprve spočítat pravděpodobnost p(n), že všech n narozenin je rozdílných. Pro n > 365 je tato pravděpodobnost, s ohledem na Dirichletův princip, rovna nule. Pro n ≤ 365 je dána vzorcem:

${\displaystyle {\begin{aligned}{\bar {p}}(n)&=1\cdot \left(1-{\frac {1}{365}}\right)\cdot \left(1-{\frac {2}{365}}\right)\cdots \left(1-{\frac {n-1}{365}}\right)=\\&={365\cdot 364\cdots (365-n+1) \over 365^{n}}=\\&={365! \over 365^{n}(365-n)!}\end{aligned}}}$

Protože druhá osoba nemůže mít stejné narozeniny jako první (364/365), třetí nemůže mít stejné narozeniny jako první dvě (363/365), atd.

Skutečnost, že nejméně dva z n lidí mají stejné narozeniny je komplementární jevu, že všechna data narozenin jsou různá. Proto pravděpodobnost p(n) je

${\displaystyle p(n)=1-{\bar {p}}(n).}$

Tato pravděpodobnost překračuje 1/2 pro n = 23 (hodnota kolem 50,7 %). Následující tabulka ukazuje pravděpodobnosti pro některé další hodnoty n (Tabulka ignoruje přestupné roky, jak již bylo výše popsáno):

Tento problém může být vypočítán také jako (1 - variace(365, počet studentů) / variace s opakováním (365, počet studentů)).