Mechanická energie

Mechanická energie je skalární fyzikální veličina, která vyjadřuje míru schopnosti tělesa konat mechanickou práci, tzn. působit silou na jiné těleso a posouvat jej po určité dráze.

Mechanická energie je jeden z mnoha druhů energie.

Mechanickou energii mají:

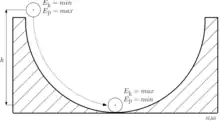
tělesa, která se vzájemně pohybují - kinetická energie (pohybová energie),
tělesa, která jsou v silových polích jiných těles - potenciální energie. Především hovoříme o tíhové potenciální energii, kterou má každé těleso v silovém poli Země,
pružná tělesa, která jsou stlačená nebo natažená - potenciální energie pružnosti (potenciální energie pružnosti).

Značení

Značka veličiny: E (angl. energy)
Jednotka: joule, značka jednotky: J
Další jednotky: kilojoule kJ, megajoule MJ, gigajoule GJ

Výpočet

Nákres pohybu koule na U-dráze. Koule je umístěna do nejvyššího polohy, výšky h, kde má maximální potenciální tíhovou energie E_p a nulovou kinetickou energii E_k. Tečkovaná šipka znázorňuje trajektorii pohybu koule po U-dráze. V nejnižším bodě koule dosahuje nejvyšší kinetické energie E_k a nulové potenciální tíhové energie E_p. V nákresu není uvažován odpor prostředí.

Celková mechanická energie je definována jako součet kinetické a potenciální energie tělesa, tzn.

E=E_{k}+E_{p}

.

Zákon zachování mechanické energie

Přeměna mechanické energie mezi tělesy v izolované mechanické soustavě se děje konáním mechanické práce jednoho tělesa působícího na druhé a platí pro ni zákon zachování mechanické energie, který je zvláštním případem obecného zákona zachování energie. Tento zákon lze formulovat následujícím způsobem

{\frac {dE}{dt}}=0\implies E={\text{konst.}}

.

Odvození

Pro úplný diferenciál potenciální nestacionární potenciální energie $E_{p}(\mathbf {r} ,t)$ lze psát

dE_{p}={\frac {\partial E_{p}}{\partial x}}dx+{\frac {\partial E_{p}}{\partial y}}dy+{\frac {\partial E_{p}}{\partial z}}dz+{\frac {\partial E_{p}}{\partial t}}dt=\nabla E_{p}\cdot d\mathbf {r} +{\frac {\partial E_{p}}{\partial t}}dt

.

Element práce vyjádříme jako

dW=\mathbf {F} \cdot d\mathbf {r} =-\nabla E_{p}\cdot d\mathbf {r} =-dE_{p}+{\frac {\partial E_{p}}{\partial t}}dt

,

odkud pak dostáváme vztah pro okamžitý výkon ve tvaru

{\frac {dW}{dt}}=\mathbf {F} \cdot \mathbf {v} =-\nabla E_{p}\cdot \mathbf {v} =-{\frac {dE_{p}}{dt}}+{\frac {\partial E_{p}}{\partial t}}

.

Dále předpokládejme, že na hmotný bod působí nestacionární potenciálová síla, disipativní síla a gyroskopická síla. Celkovou sílu lze psát ve tvaru

\mathbf {F} =-\nabla E_{p}+\mathbf {F} _{Gy}+\mathbf {F} _{Dis}

.

Pro okamžitý výkon výslednice uvažovaných sil můžeme psát (připomeňme, že gyroskopické síly jsou kolmé na vektor pohybu)

{\frac {dW}{dt}}=\mathbf {F} \cdot \mathbf {v} =-\nabla E_{p}\cdot \mathbf {v} +\mathbf {F} _{Gy}\cdot \mathbf {v} +\mathbf {F} _{Dis}\cdot \mathbf {v} =-{\frac {dE_{p}}{dt}}+{\frac {\partial E_{p}}{\partial t}}+\mathbf {F} _{Dis}\cdot \mathbf {v}

.

Ze vztahu kinetické energie a okamžitého výkonu víme, že platí rovnost

{\frac {dW}{dt}}={\frac {dE_{k}}{dt}}

,

s jejíž pomocí předchozí vztah upravíme následujícím způsobem

{\frac {dE_{k}}{dt}}=-{\frac {dE_{p}}{dt}}+{\frac {\partial E_{p}}{\partial t}}+\mathbf {F} _{Dis}\cdot \mathbf {v} \implies {\frac {d(E_{k}+E_{p})}{dt}}={\frac {\partial E_{p}}{\partial t}}+\mathbf {F} _{Dis}\cdot \mathbf {v}

.

Protože jsou disipativní síly záporné $\mathbf {F} _{Dis}\cdot \mathbf {v} =-kv^{2},k>0$ , tak se podílejí na úbytku celkové mechanické energie, přičemž z toho vyplývá za předpokladu stacionárních potenciálových sil, že změna celkové energie je spojena pouze s jejím úbytkem.

{\frac {dE}{dt}}=\mathbf {F} _{Dis}\cdot \mathbf {v} =-kv^{2}

.

Pokud ke všemu nebudou na hmotný bod působit žádné disipativní síly (např. odpor prostředí), pak dostáváme zákon zachování mechanické energie v izolované soustavě ve tvaru

{\frac {dE}{dt}}=0\implies E={\text{konst.}}

.

Odkazy

Související články

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.