Lawsonovo kritérium
Lawsonovo kritérium vyjadřuje energetickou bilanci reakce jaderné fúze.
Původní formulace
Britský fyzik J. D. Lawson publikoval v roce 1955 (odtajněno 1957) původní vyjádření kritéria energetické bilance fúzních elektráren, čímž byl dán základ pro reálné šance na využití jaderné fúze v energetice[1]. V tomto článku zavádí parametr R, kterým vyjadřuje poměr uvolněné energie ku energii dodané.
PR vyjadřuje získaný výkon, PB ztráty energie. Obě tyto hodnoty jsou závislé na druhé mocnině hustoty n2 a parametr R se tak stává funkcí teploty, hustoty a času. Původní Lawsonova formulace zahrnuje dobu trvání výboje t, zatímco v dnešním tvaru se počítá s dobou udržení 𝜏E. Při podmínkách pro uskutečnění termojaderné fúze se materiál paliva nachází ve skupenství plazmatu. Doba udržení 𝜏E je poměr energie plazmatu ku ztrátovému výkonu PL.
Následně počítá s účinností návratu energie do systému 1/3, z čehož plyne kritérium R>2.
Původní formulace odvozená z této bilance má tvar:
EF vyjadřuje energii získanou fúzní reakcí, <σv> je fúzní reaktivita.
Fúzní reaktivita
Fúzní reaktivita charakterizuje fúzní palivo, hodnota reaktivity je závislá na teplotě T. Hodnotu určujeme pomocí metodik, které vychází z experimentálně naměřených dat. Zmíněné metodiky dochází ke srovnatelným hodnotám reaktivit, nejvíce různých reakcí popisuje metoda polynomu[2].
Některé z metodik pro stanovení fúzní reaktivity:
Druhy kritérií
V současné době se rozlišují tři rovnice Lawsonova kritéria pro různé energetické rovnováhy:
- Scientific Breakeven (vědecké vyrovnání) - výkon uvolněný fúzní reakcí se rovná výkonu ohřevu plazmatu. Energetická bilance popsaná tímto kritériem se týká pouze plazmatu a nezahrnuje další procesy, např. účinnost přeměny uvolněného výkonu na výkon technicky využitelný.
- Ignition (zapálení) - fúzní výkon přenášený alfa částicemi zachycenými v plazmatu vyrovnává ztráty plazmatu. Plazma se tak samo ohřívá a vnější ohřev plazmatu již není potřebný. Energetická bilance popsaná tímto kritériem se týká pouze plazmatu a nezahrnuje další procesy, stejně jako v přechozím případě.
- Engineering Breakeven (inženýrské vyrovnání) - stav, kdy hrubý elektrický výkon elektrárny po odpočtu vlastní spotřeby elektrárny přesáhne příkon potřebný k ohřevu plazmatu. Na rozdíl od vědeckého vyrovnání tato energetická bilance zahrnuje celou elektrárnu[5]. Pokud je kritérium splněno, fúzní elektrárna je energeticky zisková a může dodávat energii do rozvodné sítě. Pokud příkon ohřevu zahrneme do vlastní spotřeby elektrárny, pak je kritérium obvyklou energetickou bilancí elektrárny, ve které se čistý výstupní výkon rovná rozdílu hrubého výkonu a vlastní spotřeby.
Seznam fúzních reakcí
Neutronové reakce:
(produkty reakce D+D mohou být , nebo s pravděpodobností 50:50)
Aneutronové reakce:
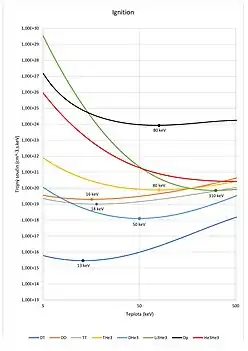
Lawsonovo kritérium
pro stav Ignition
Vyjádření požadavku na rovnost mezi energií uvolněnou alfa částicemi a ztrátovým výkonem PL (alfa částice nesou 1/5 uvolněného fúzního výkonu PF, protože hmotnost neutronu, který uniká z magnetického pole tokamaku a odnáší 4/5 uvolněné energie pryč, je ve srovnání s hmotností alfa částice přibližně pětinová, a platí zákon zachování hybnosti):
Ztrátový výkon:
Fúzní výkon:
Dosazení do bilance výkonů:
Upravení do tvaru tzv. trojného součinu:
Odstraněním Boltzmannovy konstanty převedeme z jednotky kelvin do jednotky elektronvolt:
pro stav Scientific breakeven
pro stav Engineering breakeven
Koeficient vyjadřuje účinnost, se kterou dokáže elektrárna přeměnit výkon uvolněný fúzní reakcí na výstupní výkon celého systému. Při teoretické 100% účinnosti (=1) by kritérium inženýrské rovnováhy bylo shodné s kritériem ignition. Kriteriální rovnice se mohou uvádět i ve tvaru počítajícím s průměrnou teplotou , ta je při předpokladu parabolického průběhu rovna poloviční hodnotě teploty T (maximální teplota v palivu), rovnice tak nabývá tvar:
Faktor zesílení Q
Pro hodnocení energetické bilance fúzních reaktorů se používá faktor zesílení. Faktor zesílení je poměr fúzního výkonu ku výkonu ohřevu . Hodnota faktoru Q=1 je významnou hranicí, kdy začíná docházet k energetickému zisku, tento bod znamená dosažení stavu scientific breakeven (vědecké vyrovnání) nebo jen zkráceně breakeven. Tokamak JET dosáhl v roce 1997 faktoru zesílení Q=0,67, cílem současného projektu ITER je dosažení Q=10. Pro budoucí projekt demonstrační fúzní elektrárny DEMO se uvažuje hodnota až Q=25. Doposud nebylo na žádném zařízení dosaženo hodnoty Q=1[6].
Maximální dosažitelná hodnota faktoru zesílení je závislá na poloměru a síle magnetického pole konkrétního reaktoru[7]. Zatím nelze zkonstruovat malý reaktor, který bude funkčním modelem budoucí fúzní elektrárny. Nejprve je nutné na menších (energeticky ztrátových) zařízeních postupně získávat zkušenosti a následně bude možné investovat do vybudování demonstrační elektrárny DEMO o plných rozměrech.
Závěr
Z Lawsonova kritéria plyne, že nejsnáze dosažitelná je fúzní reakce deuteria a tritia ( reakce), při teplotě okolo 160 mil. stupňů. patří mezi reakce, během kterých dochází k produkci neutronů. Produkce neutronů ve fúzním reaktoru způsobuje aktivaci materiálů konstrukce a komplikuje tak významně jeho provoz. Reakce, při kterých neutrony nevznikají, jsou pro energetiku mnohem vhodnější, ale z Lawsonova kritéria vyplývá, že je k jejich dosažení potřeba mnohem vyšších parametrů reaktoru.
Reference
- LAWSON, J D. Some Criteria for a Power Producing Thermonuclear Reactor. Proceedings of the Physical Society. Section B. 1957-01-01, roč. 70, čís. 1, s. 6–10. Dostupné online [cit. 2020-10-12]. ISSN 0370-1301. DOI 10.1088/0370-1301/70/1/303.
- NAYAK, Bishnupriya. Reactivities of neutronic and aneutronic fusion fuels. Annals of Nuclear Energy. 2013-10, roč. 60, s. 73–77. Dostupné online [cit. 2020-10-13]. DOI 10.1016/j.anucene.2013.04.025. (anglicky)
- MOSES, Gregory A.; SANTARIUS, John F. High Energy Density Simulations for Inertial Fusion Energy Reactor Design. Fusion Science and Technology. 2005-05-01, roč. 47, čís. 4, s. 1121–1125. Dostupné online [cit. 2020-10-13]. ISSN 1536-1055. DOI 10.13182/fst05-a836.
- BOSCH, H.-S; HALE, G.M. Improved formulas for fusion cross-sections and thermal reactivities. Nuclear Fusion. 1993-12, roč. 33, čís. 12, s. 1919–1919. Dostupné online [cit. 2020-10-13]. ISSN 0029-5515. DOI 10.1088/0029-5515/33/12/513.
- ENTLER, Slavomír. Engineering Breakeven. Journal of Fusion Energy. 2015-06-01, roč. 34, čís. 3, s. 513–518. Dostupné online [cit. 2020-10-13]. ISSN 1572-9591. DOI 10.1007/s10894-014-9830-2. (anglicky)
- Plasma physics | The Tao of Q. ITER [online]. [cit. 2020-10-20]. Dostupné online. (anglicky)
- ZOHM, Hartmut. On the size of tokamak fusion power plants. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2019-03-25, roč. 377, čís. 2141, s. 20170437. Dostupné online [cit. 2020-10-28]. DOI 10.1098/rsta.2017.0437. PMID 30967051.