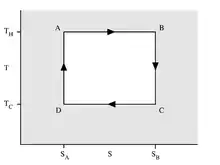
Carnotův cyklus

Carnotovův cyklus se skládá ze čtyř fází.

1. Izotermická expanze

Z počátečního stavu plynu, který je dán tlakem ${\displaystyle p_{1}}$, objemem ${\displaystyle V_{1}}$ a teplotou ${\displaystyle T_{1}}$ se plyn izotermicky rozpíná. Při tomto rozpínání plyn vykoná na úkor dodaného tepla ${\displaystyle Q_{1}}$ práci ${\displaystyle W_{12}}$. Teplo ${\displaystyle Q_{1}}$ je dodáno z okolí (tzv. ohřívač). Vztah mezi prací a teplem lze zapsat ve tvaru ${\displaystyle -W_{12}=Q_{1}}$.

Na konci této fáze cyklu je stav plynu popsán stavovými veličinami ${\displaystyle p_{2}}$, ${\displaystyle V_{2}}$ a ${\displaystyle T_{1}}$, pro něž platí, že ${\displaystyle p_{2}<p_{1}}$ a ${\displaystyle V_{2}>V_{1}}$.

2. Adiabatická expanze

Adiabatická expanze navazuje na izotermickou expanzi. Počáteční stav adiabatické expanze je dán stavovými veličinami ${\displaystyle p_{2}}$, ${\displaystyle V_{2}}$ a ${\displaystyle T_{1}}$, které jsou konečným stavem izotermické expanze. Při adiabatickém rozpínání nedochází k výměně tepla s okolím. Práce ${\displaystyle W_{23}}$, kterou plyn vykoná v této fázi cyklu jde na úkor vnitřní energie, tzn. ${\displaystyle W_{23}=U_{2}-U_{3}}$. Snížením vnitřní energie dojde také k poklesu teploty plynu.

Na konci této fáze cyklu je stav plynu popsán stavovými veličinami ${\displaystyle p_{3}}$, ${\displaystyle V_{3}}$ a ${\displaystyle T_{3}}$, pro něž platí, že ${\displaystyle p_{3}<p_{2}}$, ${\displaystyle V_{3}>V_{2}}$ a ${\displaystyle T_{3}<T_{1}}$.

3. Izotermická komprese

Izotermická komprese navazuje na adiabatickou expanzi. Počáteční stav izotermické komprese je dán stavovými veličinami ${\displaystyle p_{3}}$, ${\displaystyle V_{3}}$ a ${\displaystyle T_{3}}$, které jsou konečným stavem adiabatické expanze. Při izotermickém stlačování vykonáváme na plynu práci, která se odevzdává okolí ve formě tepla. Dodaná práce ${\displaystyle W_{34}}$ je rovna uvolněnému teplu, tzn. ${\displaystyle W_{34}=-Q_{3}}$.

Na konci této fáze cyklu je stav plynu popsán stavovými veličinami ${\displaystyle p_{4}}$, ${\displaystyle V_{4}}$ a ${\displaystyle T_{3}}$, pro něž platí, že ${\displaystyle p_{4}>p_{3}}$ a ${\displaystyle V_{4}<V_{3}}$.

4. Adiabatická komprese

Adiabatická komprese navazuje na izotermickou kompresi. Počáteční stav adiabatické komprese je dán stavovými veličinami ${\displaystyle p_{4}}$, ${\displaystyle V_{4}}$ a ${\displaystyle T_{3}}$, které jsou konečným stavem izotermické komprese. Při adiabatické kompresi stlačujeme plyn, který je dokonale tepelně izolován. Nedochází tedy k výměně tepla s okolím. Práce ${\displaystyle W_{41}}$, kterou dodáme plynu, je spotřebována na zvýšení vnitřní energie plynu, tzn. ${\displaystyle W_{41}=U_{4}-U_{1}}$.

Protože se jedná o uzavřený cyklus, je na konci této fáze cyklu stav plynu určen stavovými veličinami ${\displaystyle p_{1}}$, ${\displaystyle V_{1}}$ a ${\displaystyle T_{1}}$.

Celková práce ${\displaystyle W}$, kterou soustava během cyklu vykonala, je ${\displaystyle W=W_{12}+W_{23}+W_{34}+W_{41}}$. Poněvadž však je ${\displaystyle U_{1}=U_{2}}$ (vnitřní energie na počátku adiabatické expanze je stejná jako na konci adiabatické komprese, neboť se při izotermické expanzi nezměnila) a ${\displaystyle U_{3}=U_{4}}$ (vnitřní energie je stejná na konci adiabatické expanze jako na počátku adiabatické komprese, neboť se při izotermické kompresi nezměnila), platí ${\displaystyle W_{23}+W_{41}=0}$ neboli ${\displaystyle W=W_{12}+W_{34}}$, což lze zapsat ve tvaru

${\displaystyle W=Q_{1}-Q_{3}}$

Práce vykonaná soustavou při Carnotově cyklu je rovna rozdílu tepla přijatého a tepla odevzdaného.

Pokud cyklus probíhá v popsaném pořadí, pak koná soustava práci a představuje ideální tepelný motor, v němž je část tepla dodaného ohřívačem přeměněna na mechanickou práci a část se vždy odevzdá chladiči. Při opačném chodu Carnotova cyklu dostaneme ideální chladicí stroj, který teplo odnímá chladnější lázni a přenáší je na teplejší lázeň, k čemuž je nutné vykonat na soustavě práci.

Účinnost stroje je poměr výkonu a příkonu neboli poměr vykonané práce a energie dodané během jednoho cyklu. V případě Carnotova cyklu to znamená

${\displaystyle \eta ={\frac {W}{Q_{1}}}={\frac {Q_{1}-Q_{3}}{Q_{1}}}}$,

kde ${\displaystyle W}$ je celková práce, kterou soustava během cyklu vykoná, ${\displaystyle Q_{1}}$ je teplo dodané soustavě ve fázi izotermické expanze a ${\displaystyle Q_{3}}$ je teplo uvolněné soustavou při izotermické kompresi.

Podrobnějším výpočtem práce nebo použitím veličiny entropie lze získat jednoduchý vztah

${\displaystyle {\frac {Q_{1}}{Q_{2}}}={\frac {T_{1}}{T_{2}}},}$

z něhož pro účinnost plyne

${\displaystyle \eta ={T_{1}-T_{2} \over T_{1}}=1-{\frac {T_{2}}{T_{1}}}}$,

kde T₁ je termodynamická teplota ohřívače a T₂ chladiče.

Účinnost vratného Carnotova cyklu tak závisí pouze na poměru termodynamických teplot, mezi nimiž tepelný stroj pracuje. Účinnost není závislá na druhu použitého plynu, konstrukci stroje atd.

Lze dokázat, že účinnost libovolného nevratného cyklu je vždy menší než účinnost vratného cyklu. To je možné provést pomocí systému dvou tepelných strojů, vratného a nevratného. Kdyby totiž účinnost nevratného tepelného stroje byla větší než účinnost vratného tepelného stroje, bylo by možné sestrojit perpetuum mobile druhého druhu, což není možné. Pokud by byla účinnost obou strojů (vratného a nevratného) stejná, byl by celý výsledný cyklus vratný, což je v rozporu s předpokladem nevratnosti jednoho ze strojů. Jedinou možností tedy je, že účinnost nevratného tepelného stroje je nižší než účinnost vratného tepelného stroje, tzn.

${\displaystyle \eta _{nevrat}<\eta _{vrat}}$

Podle předchozích vztahů tedy platí

${\displaystyle \eta _{nevrat}={\frac {W_{nevrat}}{Q_{nevrat}}}<{\frac {T-T_{0}}{T}}}$,

který říká, že práce, kterou vykoná nevratný stroj při přechodu tepla z teplejšího tělesa na těleso chladnější, nepostačuje k převedení tepla v opačném směru.

Důsledkem druhé hlavní věty termodynamiky je tzv. Carnotova věta.

Účinnost všech vratných cyklů, které pracují mezi stejnými teplotami, je stejná a závisí pouze na teplotách obou zásobníků tepla; účinnost libovolného nevratného cyklu nemůže být větší než účinnost vratného Carnotova cyklu pracujícího mezi týmiž maximálními teplotami jako nevratný cyklus.

• Účinnost
• Druhá věta termodynamická
• Nicolas Léonard Sadi Carnot

• Obrázky, zvuky či videa k tématu Carnotův cyklus na Wikimedia Commons
• Příklady na Carnotův cyklus