Cantorova funkce

Cantorova funkce je příkladem funkce, která je spojitá (dokonce i stejnoměrně spojitá), ale není absolutně spojitá. Je pojmenována po Georgi Cantorovi.

Definice

Cantorovu funkci c : [0;1] → [0;1] zavedeme pomocí následujícího postupu:

  1. Číslo x zapíšeme v trojkové soustavě, pokud je to možné, vyhneme se zápisu, který obsahuje jedničky. (Rozdíl se projeví v případě, že rozvoj čísla končí na 022222... = 100000... nebo 200000... = 122222...)
  2. První jedničku nahradíme dvojkou a vše za ní nulou. Pokud se v zápisu čísla žádná jednička nevyskytuje, tento krok přeskočíme.
  3. Všechny dvojky nahradíme jedničkami.
  4. Výsledek interpretujeme jako číslo v binární soustavě. Toto je c(x).

Příklad:

  • 1/4 zapíšeme v trojkové soustavě jako 0,02020202...; nejsou zde žádné jedničky k nahrazení, takže můžeme rovnou přepsat dle dalšího kroku na 0,01010101...; toto (přečteno jako číslo dvojkové soustavy) se rovná 1/3. c(1/4) = 1/3.
  • 1/5 zapíšeme jako 0,01210121...; první jedničku zaměníme za dvojku a vše za ní přepíšeme nulami, získáme číslo 0.02000000...; dále přepíšeme na 0,01000000...; přečteme jako 1/4. c(1/5) = 1/4.

(Na obrázku je vidět výsledná funkce)

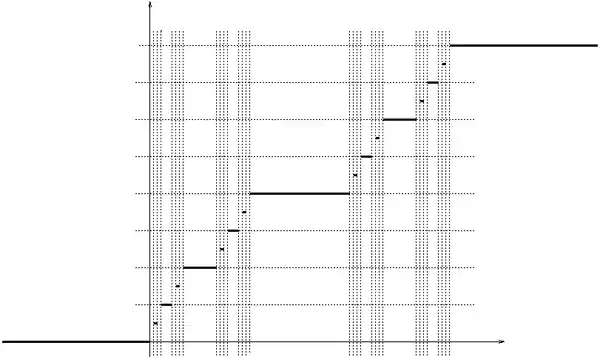
Cantorova funkce

Vlastnosti
  • Cantorova funkce je spojitá na celém intervalu [0;1]
  • zobrazuje interval [0;1] na interval [0;1]
  • má derivaci rovnou 0 skoro všude
  • je spojitá, ale není absolutně spojitá
  • nemá derivaci v žádném bodě Cantorova diskontinua
  • je konstantní na intervalech tvaru (0,x1x2x3...xn022222...; 0,x1x2x3...xn200000...), každý bod, jenž nenáleží Cantorovu diskontinuu, leží v jednom z těchto intervalů, takže jeho derivace je rovna 0.

Jiná definice
Sekvenční Cantorova funkce

Definujme posloupnost funkcí fn na intervalu [0;1] takto:

  • f0(x) = x
  • definujme fn+1(x) rekurentně pomocí fn(x)
    • fn+1(x) = 0,5 fn(3x) pokud 0 ≤ x ≤ 1/3.
    • fn+1(x) = 0,5 pokud 1/3 ≤ x ≤ 2/3.
    • fn+1(x) = 0,5 + 0.5 fn(3 (x − 2/3)) pokud 2/3 ≤ x ≤ 1.

Takto definovaná posloupnost funkcí konverguje k Cantorově funkci. Povšimněme si, že na volbě počáteční funkce nezáleží, pokud bude omezená a bude splňovat: f0(0) = 0 a f0(1) = 1

Související články

Externí odkazy
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.