Besselova funkce
Besselova funkce je řešení Besselovy rovnice
pro libovolné reálné číslo , které je označováno jako řád Besselovy funkce. Funkce je pojmenována na počest německého matematika a fyzika Friedricha Wilhelma Bessela, který ji poprvé popsal.
Cylindrické funkce
Cylindrickou funkcí se nazývá libovolné řešení Besselovy rovnice
Besselova funkce
Není-li celé číslo, pak lze obecné řešení Besselovy rovnice zapsat jako
- ,
kde a jsou lineárně nezávislé Besselovy funkce a jsou libovolné konstanty.
Besselovy funkce bývají také nazývány Besselovými funkcemi prvního druhu.
Besselova funkce řádu je definována vztahem
- ,
kde je gama funkce.
Je-li celé číslo, pak platí
- ,
výše uvedená řešení tedy nejsou v tomto případě nezávislá.
Pro lze Besselovu funkci vyjádřit v integrálním tvaru
Platí následující rekurentní vztahy
Neumannova funkce
Je-li celé číslo, pak a nejsou lineárně nezávislé. V takovém případě má obecný integrál tvar
- ,
kde je tzv. Neumannova funkce (někdy též Weberova funkce), které jsou také řešením Besselovy rovnice.
Pro Neumannovy funkce se používá označení Besselovy funkce druhého druhu.
Neumannovy funkce jsou pro celočíselná definovány vztahem
Pro různé od celého čísla je pak Neumannova funkce definována vztahem
Je-li celé číslo, pak platí
Mezi Besselovými a Neumannovými funkcemi platí vztah
Platí následující rekurentní vztahy
Hankelova funkce
Důležitými cylindrickými funkcemi jsou tzv. Hankelovy funkce a , které jsou definovány jako
Hankelova funkce bývá také označována jako Besselova funkce třetího druhu.
Sférické cylindrické funkce
Sférickou cylindrickou funkcí nazveme každé řešení rovnice
Za dvě nezávislá řešení lze zvolit sférickou Besselovu funkci
a sférickou Neumannovu funkci
- ,
kde jsou Besselovy funkce a jsou Neumannovy funkce.
Mezi sférickými Besselovými a sférickými Neumannovými funkcemi platí vztah
Jinou dvojicí nezávislých řešení jsou sférické Hankelovy funkce
Sférické cylindrické funkce lze vyjádřit následujícími vztahy
Lze ukázat, že platí
Modifikovaná Besselova funkce
Modifikované Besselovy funkce jsou řešením modifikované Besselovy rovnice
Modifikovaná Besselova funkce prvního druhu
Není-li celé číslo, pak má řešení modifikované Besselovy rovnice tvar
- ,
kde je modifikovaná Besselova funkce prvního druhu, která je definována vztahem
Modifikovanou Besselovu funkci lze vyjádřit pomocí Besselovy funkce jako
Modifikovaná Besselova funkce druhého druhu
Pro celá platí
Pro celá tedy nejsou a lineárně nezávislé funkce a obecné řešení modifikované Besselovy rovnice je nutné vyjádřit ve tvaru
- ,
kde je modifikovaná Besselova funkce druhého druhu (označovaná též jako MacDonaldova funkce).
Pro necelé je definováno
Pro celá pak platí
Fresnelův ohyb světla na hraně
Důležitým příkladem Besselovy funkce je Fresnelův ohyb světla na hraně.
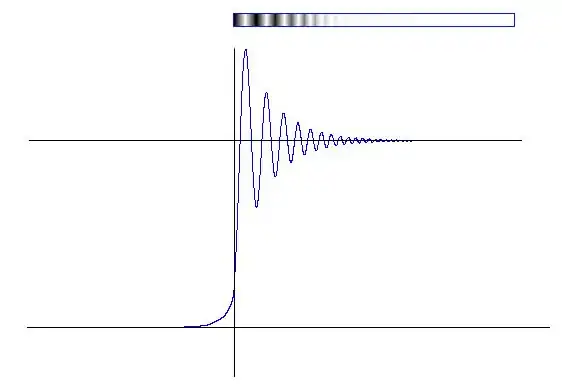
V případě osvětlení monochromatickým světlem dochází při ohybu na hraně ke vzniku ohybových proužků, které jsou rovnoběžné s přímou hranou.
V horní části je zobrazen pozorovaný jev, a ve spodní části je rozdělení intenzity světla.
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu Besselova funkce na Wikimedia Commons
Obrázky, zvuky či videa k tématu Besselova funkce na Wikimedia Commons
Literatura
- Rektorys, K. a spol.: Přehled užité matematiky I.. Prometheus, Praha, 2003, 7. vydání. ISBN 80-7196-179-5